
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n∥β,α⊥β,则m⊥n | ||
| C. | 若α∩β=l,m∥α,m∥β,则m∥l | D. | 若α∩β=m,α∩γ=n,l⊥m,l⊥n,则l⊥α |
分析 根据常见几何体模型举出反例,或者证明结论.
解答 解:(A)若m∥α,n∥α,则m与n可能平行,可能相交,也可能异面,故A错误;
(B)在正方体ABCD-A′B′C′D′中,设平面ABCD为平面α,平面CDD′C′为平面β,直线BB′为直线m,直线A′B为直线n,
则m⊥α,n∥β,α⊥β,但直线A′B与BB′不垂直,故B错误.
(C)设过m的平面γ与α交于a,过m的平面θ与β交于b,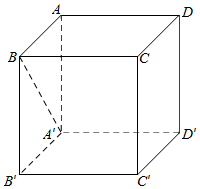
∵m∥α,m?γ,α∩γ=a,
∴m∥a,
同理可得:m∥b.
∴a∥b,∵b?β,a?β,
∴a∥β,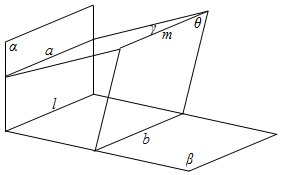
∵α∩β=l,a?α,∴a∥l,
∴l∥m.
故C正确.
(D)在正方体ABCD-A′B′C′D′中,设平面ABCD为平面α,平面ABB′A′为平面β,平面CDD′C′为平面γ,
则α∩β=AB,α∩γ=CD,BC⊥AB,BC⊥CD,但BC?平面ABCD,故D错误.
故选:C.
点评 本题考查了空间线面位置关系的判断,借助常见空间几何模型举出反例是解题关键.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:选择题
| A. | “x=5”是“x2-4x-5=0”的充分不必要条件 | |
| B. | 若p∨q为真命题,则p∧q为真命题 | |
| C. | 命题“x<-1,则x2-2x-3>0”的否命题为“若x<-1,则x2-2x-3≤0” | |
| D. | 若命题p:?x∈R,使x2+x+1<0,则¬p:?x∈R,使x2+x+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{5}$) | B. | ($\sqrt{5}$,$\sqrt{13}$) | C. | (1,2$\sqrt{5}$) | D. | (2$\sqrt{3}$,2$\sqrt{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
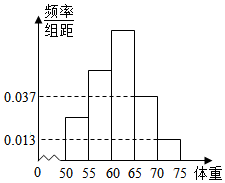 为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com