
分析 (Ⅰ)根据绝对值的几何意义求出f(x-1)+f(x)的最小值,从而求出a的范围;(Ⅱ)根据分析法证明即可.
解答 解:(Ⅰ)因为f(x-1)+f(x)=|x-4|+|x-3|≥|x-4+3-x|=1,
不等式f(x-1)+f(x)<a的解集为空集,
则1≥a即可,所以实数a的取值范围是(-∞,1].…(5分)
(Ⅱ)$\frac{f(ab)}{|a|}>f(\frac{b}{a})$,
证明:要证$\frac{f(ab)}{|a|}>f(\frac{b}{a})$,
只需证|ab-3|>|b-3a|,
即证(ab-3)2>(b-3a)2,
又(ab-3)2-(b-3a)2=a2b2-9a2-b2+9=(a2-1)(b2-9).
因为|a|<1,|b|<3,
所以(ab-3)2-(b-3a)2>0,
所以原不等式成立.…(10分)
点评 本题考查了绝对值的几何意义,考查不等式的大小比较,是一道中档题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $1+\sqrt{2}$ | B. | $1-\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $3-2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
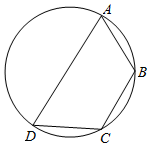 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )| A. | $\sqrt{3}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{3}}{2}$+$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n∥β,α⊥β,则m⊥n | ||
| C. | 若α∩β=l,m∥α,m∥β,则m∥l | D. | 若α∩β=m,α∩γ=n,l⊥m,l⊥n,则l⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 猪编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 181 | 166 | 185 | 180 |
| y | 95 | 100 | 97 | 103 | 101 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2.2 | 4.3 | 4.5 | 4.8 | 6.7 |
| A. | 5.76 | B. | 6.8 | C. | 8.3 | D. | 8.46 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com