
【题目】已知函数![]() 与
与![]() 互为相反数,且
互为相反数,且![]() ,函数
,函数![]() 的定义域为
的定义域为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值域;
的值域;
(3)若函数![]() 的最大值为
的最大值为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)a=log32.(2)[﹣2,0].(3)λ![]() .
.
【解析】
(1)先求得![]() ,再根据f(a+2)=18计算a;
,再根据f(a+2)=18计算a;
(2)令t=2x,结合二次函数闭区间上最值的求解即可.
(3)讨论对称轴与区间[1,2]的关系得出h(t)的单调性,根据最大值为![]() 计算λ.
计算λ.
(1)由题意函数![]() 与
与![]() 互为相反数,∴
互为相反数,∴![]() ,
,
又∵f(a+2)=3a+2=18,∴3a=2,即a=log32.
(2)当![]() 时,由(1)可知
时,由(1)可知![]() ,
,
令t=2x,
由x∈[0,1]可得t∈[1,2],g(t)=t﹣t2在[1,2]上单调递减,
故当t=1时有最大值0,t=2时有最小值﹣2,
故值域[﹣2,0].
(3)∵函数![]() 的最大值为
的最大值为![]() ,由(2)可知:即为h(t)=﹣t2+λt,t∈[1,2]的最大值为
,由(2)可知:即为h(t)=﹣t2+λt,t∈[1,2]的最大值为![]() ,
,
①若![]() 2即λ≥4,则h(t)在[1,2]上单调递增,
2即λ≥4,则h(t)在[1,2]上单调递增,
∴h(2)=﹣4+2λ![]() ,解得λ
,解得λ![]() (舍).
(舍).
②若![]() 1即λ≤2时,则h(t)在[1,2]上单调递减,
1即λ≤2时,则h(t)在[1,2]上单调递减,
∴h(1)=﹣1+λ![]() ,解得λ
,解得λ![]() (舍).
(舍).
③若1![]() 2,即2<λ<4,则h(t)在[1,2]上先增后减,
2,即2<λ<4,则h(t)在[1,2]上先增后减,
∴h(![]() )
)![]() ,解得λ
,解得λ![]() (舍负).
(舍负).
综上,λ![]() .
.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】我国明代珠算家程大位的名著《直指算法统宗》中有如下问题:“今有白米一百八十石,令三人从上及和减率分之,只云甲多丙米三十六石,问:各该若干?”其意思为:“今有白米一百八十石,甲、乙、丙三人来分,他们分得的白米数构成等差数列,只知道甲比丙多分三十六石,那么三人各分得多少白米?”请问:乙应该分得( )白米
A. 96石B. 78石C. 60石D. 42石
查看答案和解析>>
科目:高中数学 来源: 题型:
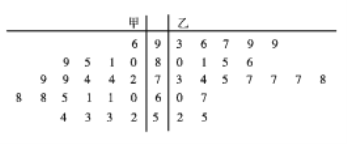
【题目】为推行“新课堂”教学法,某老师分别用传统教学和“新课堂”两种不同的教学方式在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出如图所示的茎叶图,若成绩大于70分为“成绩优良”.
(1)由统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
(2)从甲、乙两班40个样本中,成绩在60分以下(不含60分)的学生中任意选取2人,求抽取的2人中恰有一人来自乙班的概率.
|
|
|
|
|
|
|
|
|
|
附:![]() ,(
,(![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,下列结论中错误的是
,下列结论中错误的是
A. ![]()
![]() , f(
, f(![]() )=0
)=0
B. 函数y=f(x)的图像是中心对称图形
C. 若![]() 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞,![]() )单调递减
)单调递减
D. 若![]() 是f(x)的极值点,则
是f(x)的极值点,则![]() (
(![]() )=0
)=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中把三角形的田称为“圭田”,把直角梯形的田称为“邪田”,称底是“广”,称高是“正从”,“步”是丈量土地的单位.现有一邪田,广分别为十步和二十步,正从为十步,其内有一块广为八步,正从为五步的圭田.若在邪田内随机种植一株茶树,求该株茶树恰好种在圭田内的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),已知
为参数),已知![]() 与圆
与圆![]() 交于
交于![]() 两点,且
两点,且![]() ,求
,求![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,![]() 平面
平面![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)过点![]() 作一平行于平面
作一平行于平面![]() 的截面,画出该截面,说明理由,并求夹在该截面与平面
的截面,画出该截面,说明理由,并求夹在该截面与平面![]() 之间的几何体的体积.
之间的几何体的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com