
分析 (1)列举出所有符合条件的元素,
(2)验证n=1时猜想是否成立,假设n=k时猜想成立,则n=k+1时,C中多出的元素是可数的,即可验证n=k+1时,猜想是否成立.
解答 解:(1)当n=1时,C={(1,1),(1,2),(1,3),(1,4),(2,2),(2,4),(2,1)},
∴f(1)=7;
当n=2时,C={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(1,7),(1,8),(2,2),(2,4),(2,6),(2,8),(2,1)},∴f(2)=13;
当n=3时,C={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(1,7),(1,8),(1,9),(1,10),(1,11),(1,12),(2,2),(2,4),(2,6),(2,8),(2,10),(2,12),(2,1)},
∴f(3)=19.
(2)猜想:f(n)=6n+1.
①当n=1时,由(1)知f(1)=7=6×1+1,结论成立;
②假设当n=k(k≥1,k∈N*)时,结论成立,即f(k)=6k+1,
那么当n=k+1时,C中新增加的元素为(1,4k+1),(1,4k+2),(1,4k+3),(1,4k+4),(2,4k+2),(2,4k+4),
所以f(k+1)=f(k)+4+2=6k+1+6=6(k+1)+1,
所以当n=k+1时,结论也成立.
根据①和②可知,f(n)=6n+1当n∈N*时都成立.
点评 本题考查了数学归纳法的证明,掌握证明步骤,发现n=k与n=k+1时的联系是证明的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
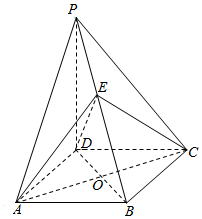 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=PD=2,O为AC与BD的交点,E为棱PB上一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=PD=2,O为AC与BD的交点,E为棱PB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com