
分析 根据角与角的关系,即可得出结论.
解答 解:归纳有:sin2a+sin2(60-a)+sinasin(60-a)=$\frac{3}{4}$
证明如下:sin260=sin2[a+(60-a)]=[sinacos(60-a)+cosasin(60-a)]2
=sin2acos2(60-a)+2sinasin(60-a)cosacos(60-a)+cos2asin2(60-a)
=sin2a[1-sin2(60-a)]+2sinasin(60-a)cosacos(60-a)+(1-sin2a]sin2(60-a)
=sin2a+sin2(60-a)]+2sinasin(60-a)[cosacos(60-a)-sinasin(60-a)]
=sin2a+sin2(60-a)]+2sinasin(60-a)[cosacos(60-a)-sinasin(60-a)]
=sin2a+sin2(60-a)]+2sinasin(60-a)cos60=sin2a+sin2(60-a)]+sinasin(60-a)=$\frac{3}{4}$.
点评 本题考查归纳推理,考查学生分析解决问题的能力,分析左边角的规律是关键.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {2,3} | C. | {1} | D. | {2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 1-$\frac{π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
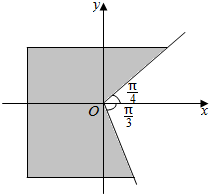
| A. | {a|$\frac{π}{4}$≤a≤$\frac{π}{3}$} | B. | {a|$\frac{π}{4}$≤a≤$\frac{5π}{3}$} | ||
| C. | {a|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{π}{3}$,k∈Z} | D. | {a|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{5π}{3}$,k∈Z} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com