
分析 (1)当a=1时,利用集合的基本运算求M∪N及N∩∁RM;
(2)利用x∈M是x∈N的充分条件,即可求实数a的取值范围.
解答 解:(1)N={x|x2-2x-3≤0}={x|-1≤x≤3},
当a=1时,M={x|-a<x<a+1,a∈R}={x|-1<x<2},
∴M∪N={x|-1≤x≤3}∪{x|-1<x<2}={x-1≤x≤3},
N∩∁RM={x|x=-1或2≤x≤3};
(2)∵N={x|-1≤x≤3},M={x|-a<x<a+1,a∈R},
若x∈M是x∈N的充分条件,
则M⊆N,
若M=∅,即-a≥a+1,即a≤-$\frac{1}{2}$时,满足条件.
若M≠∅,要使M⊆N,
则 $\left\{\begin{array}{l}{-a<a+1}\\{-a≥-1}\\{a+1≤3}\end{array}\right.$,即 $\left\{\begin{array}{l}{a>-\frac{1}{2}}\\{a≤1}\\{a≤2}\end{array}\right.$,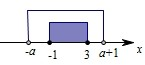
∴-$\frac{1}{2}$<a≤1,
综上:a≤1.
点评 本题主要考查集合的基本运算,以及充分条件和必要条件的应用,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | an=$\frac{2n}{\frac{7}{9}(1{0}^{n}-1)}$ | B. | an=$\frac{18n-9}{7(1{0}^{n}-1)}$ | C. | an=$\frac{2n-1}{7(1{0}^{n}-1)}$ | D. | an=$\frac{2n-1}{\frac{7}{8}({8}^{n}-1)}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 班级 | 1 | 2 | 3 | 4 | 5 | 6 |
| 频数 | 6 | 10 | 12 | 12 | 6 | 4 |
| 达到 | 3 | 6 | 6 | 6 | 4 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin1>sin2>sin3 | B. | sin2>sin1>sin3 | C. | sin1>sin3>sin2 | D. | sin3>sin2>sin1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com