
分析 (1)利用作差法,比较$\frac{y}{x}$与$\frac{y+m}{x+m}$的大小;
(2)直接利用分析法的证明步骤,找出不等式成立的充分条件即可.
解答 (1)解:因为$\frac{y}{x}$-$\frac{y+m}{x+m}$=$\frac{m(y-x)}{x(x+m)}$,x>y>0,m>0…(2分)
所以m(y-x)<0,x(x+m)>0 …(4分)
所以$\frac{m(y-x)}{x(x+m)}$<0,即$\frac{y}{x}$-$\frac{y+m}{x+m}$<0,
所以$\frac{y}{x}$<$\frac{y+m}{x+m}$.…(6分)
(2)证明:要证用分析证明:$\sqrt{xy}$(2-$\sqrt{xy}$)≤1,
只需2$\sqrt{xy}$-($\sqrt{xy}$)2≤1,…(7分)
只需($\sqrt{xy}$)2-2$\sqrt{xy}$+1≥0,
即($\sqrt{xy}$-1)2≥0,…(9分)
因为x,y>0,且($\sqrt{xy}$-1)2≥0成立,…(11分)
所以$\sqrt{xy}$(2-$\sqrt{xy}$)≤1.…(12分)
点评 本题考查了利用综合法及分析法证明不等式,关键是掌握综合法与分析法的原理、步骤及格式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题①,②均为真命题 | B. | 命题②,③均为假命题 | ||
| C. | 命题②,④均为假命题 | D. | 命题①,③,④均为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
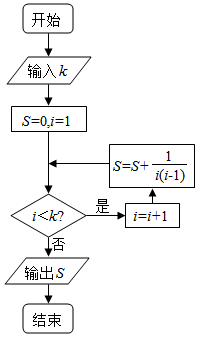
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$ | B. | 2$\overrightarrow{CB}$ | C. | 2$\overrightarrow{BC}$ | D. | $\overrightarrow{0}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com