
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要的条件 |
分析 对a分类讨论,利用两条直线相互垂直的充要条件即可得出.
解答 解:当a=0时,两条直线分别化为:x=0,4y+1=0,此时两条直线相互垂直;
当a=$\frac{3}{2}$时,此时两条直线不垂直,舍去;
当a≠0,$\frac{3}{2}$时,由于两条直线相互垂直,则$-\frac{1}{a}$×$\frac{a}{2a-3}$=-1,则a=2.
综上可得:a=0或2.
∴“a=2”是“直线l1:x+ay-a=0与直线l2:ax-(2a-3)y+1=0垂直”的充分不必要条件.
故选:A.
点评 本题考查了简易逻辑的判定方法、两条直线相互垂直的充要条件,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{2}$ | B. | 0 | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{1}{3}x+2$ | B. | $y=-\frac{1}{3}x-2$ | C. | y=-3x+2 | D. | y=3x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
| A. | 2.3 | B. | 3.2 | C. | 4.2 | D. | 2.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
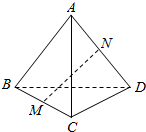 如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为30°或60°.
如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为30°或60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com