
阅读:
已知 、
、 ,
, ,求
,求 的最小值.
的最小值.
解法如下: ,
,
当且仅当 ,即
,即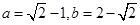 时取到等号,
时取到等号,
则 的最小值为
的最小值为 .
.
应用上述解法,求解下列问题:
(1)已知 ,
, ,求
,求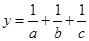 的最小值;
的最小值;
(2)已知 ,求函数
,求函数 的最小值;
的最小值;
(3)已知正数 、
、 、
、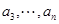 ,
, ,
,
求证: .
.
(1)9;(2)18;(3)证明见解析.
解析试题分析:本题关键是阅读给定的材料,弄懂弄清给定材料提供的方法(“1”的代换),并加以运用.主要就是 ,展开后就可应用基本不等式求得最值.(1)
,展开后就可应用基本不等式求得最值.(1)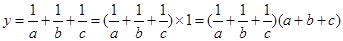 ;(2)虽然没有已知的“1”,但观察求值式子的分母,可以凑配出“1”:
;(2)虽然没有已知的“1”,但观察求值式子的分母,可以凑配出“1”: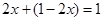 ,因此有
,因此有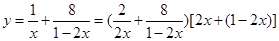 ,展开后即可应用基本不等式;(3)观察求证式的分母,结合已知有
,展开后即可应用基本不等式;(3)观察求证式的分母,结合已知有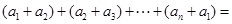
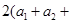
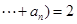 ,因此有
,因此有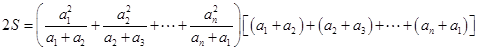
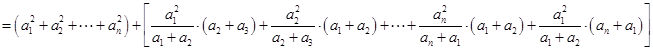 此式中关键是凑配出基本不等式所需要的两项,如
此式中关键是凑配出基本不等式所需要的两项,如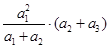 与
与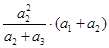 合并相加利用基本不等式有
合并相加利用基本不等式有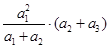
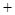
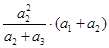
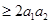 ,从而最终得出
,从而最终得出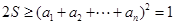 .
.
(1)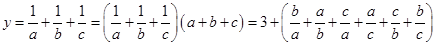 ,
,
2分
而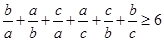 ,
,
当且仅当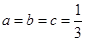 时取到等号,则
时取到等号,则 ,即
,即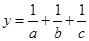 的最小值为
的最小值为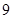 . 5分
. 5分
(2)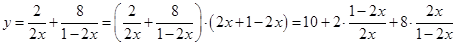 , 7分
, 7分
而 ,
,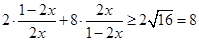 ,
,
当且仅当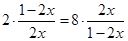 ,即
,即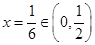 时取到等号,则
时取到等号,则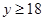 ,
,
所以函数 的最小值为
的最小值为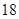 . 10分
. 10分
(3)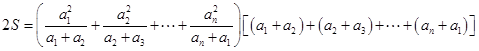
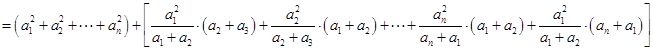
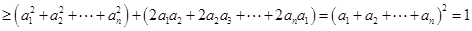
当且仅当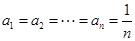 时取到等号,则
时取到等号,则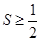 . 16分
. 16分
考点:阅读材料问题,“1”的代换,基本不等式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
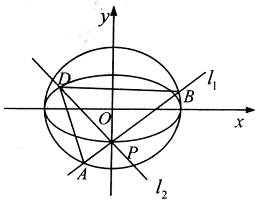
如图,点 是椭圆
是椭圆 的一个顶点,
的一个顶点, 的长轴是圆
的长轴是圆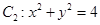 的直径,
的直径,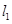 、
、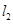 是过点
是过点 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中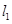 交圆
交圆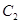 于
于 、
、 两点,
两点,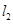 交椭圆
交椭圆 于另一点
于另一点 .
.
(1)求椭圆 的方程;
的方程;
(2)求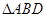 面积的最大值及取得最大值时直线
面积的最大值及取得最大值时直线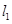 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地需要修建一条大型输油管道通过240公里宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程是在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为400万元,铺设距离为x公里的相邻两增压站之间的输油管道费用为x2+x万元.设余下工程的总费用为y万元.
(1)试将y表示成x的函数;
(2)需要修建多少个增压站才能使y最小,其最小值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com