
| A. | [6,10] | B. | [6,8] | C. | [8,10] | D. | [8,11] |
分析 设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得a=11,b=8,可得椭圆方程,设出P(m,n),代入椭圆方程,求出|OP|,由椭圆的范围可得|OP|的最值,进而得到所求范围.
解答 解:设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
可得2a=22,即a=11,
2b=16,即b=8,
则椭圆方程为$\frac{{x}^{2}}{121}$+$\frac{{y}^{2}}{64}$=1,
设椭圆的点为P(m,n),
即有$\frac{{m}^{2}}{121}$+$\frac{{n}^{2}}{64}$=1,即为n2=64(1-$\frac{{m}^{2}}{121}$),
可得|OP|=$\sqrt{{m}^{2}+{n}^{2}}$=$\sqrt{{m}^{2}+64-\frac{64}{121}{m}^{2}}$
=$\sqrt{64+\frac{57}{121}{m}^{2}}$,
由-11≤m≤11,可得m=0时,|OP|取得最小值8;
m=±11时,|OP|取得最大值11.
则椭圆上的点到椭圆中心距离的取值范围是[8,11].
故选:D.
点评 本题考查椭圆的方程和性质,主要是椭圆的范围,考查两点的距离公式和二次函数的最值求法,属于中档题.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:选择题
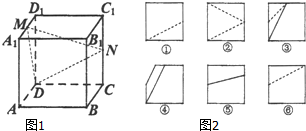
| A. | ①④⑤ | B. | ②③⑥ | C. | ①③⑤ | D. | ②④⑥ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,圆锥SO中,AB、CD为底面圆O的两条直径,AB∩CD=O,且AB⊥CD,SO=OB=2,P为SB的中点.(1)求证:SA∥平面PCD;
如图,圆锥SO中,AB、CD为底面圆O的两条直径,AB∩CD=O,且AB⊥CD,SO=OB=2,P为SB的中点.(1)求证:SA∥平面PCD;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x0∈(-4,-3) | B. | x0∈(-3,-2) | C. | x0∈(-2,-1) | D. | x0∈(-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com