
分析 (Ⅰ)设正三棱柱底面边长为a,高为h,则底面外接圆半径$R=\frac{{\sqrt{3}}}{3}a$,即可求正三棱柱与它的外接圆柱的体积之比;
(Ⅱ)内切圆半径$r=\frac{{\sqrt{3}}}{6}a$,利用内切圆柱的体积为24πcm3,求正三棱柱的底面边长.
解答 解:(Ⅰ)设正三棱柱底面边长为a,高为h,则底面外接圆半径$R=\frac{{\sqrt{3}}}{3}a$….(2分)
∴${V_{三棱柱}}=\frac{{\sqrt{3}}}{4}{a^2}h,\;\;\;\;\;\;\;{V_{外接圆柱}}=π{R^2}h=π{(\frac{{\sqrt{3}}}{3}a)^2}h=\frac{a^2}{3}πh$…..(5分)
∴$\frac{{{V_{三棱柱}}}}{{{V_{外接圆柱}}}}=\frac{{\frac{{\sqrt{3}}}{4}{a^2}h}}{{\frac{π}{3}{a^2}h}}=\frac{{3\sqrt{3}}}{4π}$….(7分)
(Ⅱ)∵内切圆半径$r=\frac{{\sqrt{3}}}{6}a$,….(8分)
∴${V_{内切圆柱}}=π{r^2}h=π{(\frac{{\sqrt{3}}}{6}a)^2}×6=\frac{a^2}{2}π=24π$…(10分)
∴${a^2}=48,a=4\sqrt{3}$
∴可求得底面边长为$4\sqrt{3}cm$.…(12分)
点评 本题考查正三棱柱与它的外接圆柱的体积之比,考查体积的计算,考查计算能力,转化思想的应用.


科目:高中数学 来源: 题型:解答题
 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
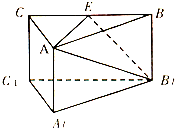 如图,三棱柱中,侧棱AA1⊥底面A1B1C1,三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱中,侧棱AA1⊥底面A1B1C1,三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | A1C1⊥平面ABB1A1 | ||
| C. | AE,B1C1为异面直线,且AE⊥B1C1 | D. | A1C1∥平面A1EB |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,过圆外一点P作直线AB的垂线,垂足为F,交圆于C,E两点,PD切圆于D,连接AD交EP于G.
如图,过圆外一点P作直线AB的垂线,垂足为F,交圆于C,E两点,PD切圆于D,连接AD交EP于G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com