考点:三角函数中的恒等变换应用,平面向量数量积的坐标表示、模、夹角
专题:综合题,三角函数的求值,平面向量及应用
分析:(1)利用向量是数量积公式,可得函数f(x)的表达式;
(2)代入函数f(x)的表达式,可求f(π)的值;
(3)由f(
α+)=
,α∈(-
,0),求出
sinα=-,cosα,再利用角的变换,即可求f(2α)的值.
解答:
解:(1)∵
=(cos(x-),0),
=(2,0),x∈R,
∴
f(x)=•=2cos(x-),即函数
f(x)=2cos(x-).(3分)
(2)
f(π)=2cos(π-)=-2cos=-(6分)
(3)∵
f(α+)=2cos(α+-)=2cos(α+)=-2sinα,
又
f(α+)=,∴
-2sinα=,即
sinα=-.(7分)
∵
α∈(-,0),∴
cosα===.(8分)
∴
sin2α=2sinαcosα=2×(-)×=-,(9分)
cos2α=2cos2α-1=2×()2-1=.(10分)
∴
f(2α)=2cos(2α-)=2cos2αcos+2sin2αsin(11分)
=
2××+2×(-)×=.(12分)
点评:本题考查向量知识的运用,考查同角三角函数关系,考查角的变换,考查小时分析解决问题的能力,属于中档题.



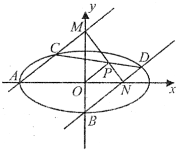 如图,过椭圆L的左顶点A(-3,0)和下顶点B且斜率均为k的两直线l1,l2分别交椭圆于C,D,又l1交y轴于M,l2交x轴于N,且CD与MN相交于点P,当k=3时,△ABM是直角三角形.
如图,过椭圆L的左顶点A(-3,0)和下顶点B且斜率均为k的两直线l1,l2分别交椭圆于C,D,又l1交y轴于M,l2交x轴于N,且CD与MN相交于点P,当k=3时,△ABM是直角三角形.