
分析 求出x<0时,函数f(x)的解析式,画出R上的图象,构造f(x)与y=$\frac{1}{π}$交点问题,利用对称性求解,注意确定交点坐标求解.
解答 解:∵定义在R上的奇函数f(x),当x≥0时,$f(x)=\left\{\begin{array}{l}\frac{-2x}{x+1},x∈[0,1)\\ 1-|x-3|,x∈[1,+∞)\end{array}\right.$,
∴x<0时,f(x)=$\left\{\begin{array}{l}{\frac{-2x}{1-x},x∈(-1,0]}\\{|x+3|-1,x∈(-∞,-1]}\end{array}\right.$画出图象:
∵函数F(x)=f(x)-$\frac{1}{π}$,
∴f(x)与y=$\frac{1}{π}$交点的横坐标,
根据图象可设交点的横坐标从左到右为x1,x2,x3,x4,x5,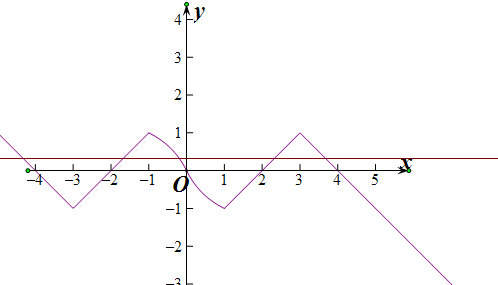
根据图象的对性可知;x1+x2=-6,x4+x5=6,
∴x1+x2=x3=x4=x5=x3,
∵$\frac{-2x}{1-x}$=$\frac{1}{π}$,x=$\frac{1}{1-2π}$,
故函数F(x)=f(x)-$\frac{1}{π}$的所有零点之和为:$\frac{1}{1-2π}$.
故答案为:$\frac{1}{1-2π}$.
点评 本题考查了函数的奇偶性,图象的对称性,函数的零点与构造函数交点的问题,属于中档题,关键是确定函数解析式,画图象.考查数形结合转化思想应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
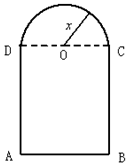 如图,用长为12m的铁丝弯成下部为矩形,上部为半圆形的框架窗户,若半圆半径
如图,用长为12m的铁丝弯成下部为矩形,上部为半圆形的框架窗户,若半圆半径查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 1+i | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
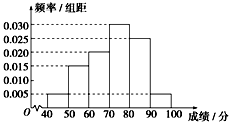 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩 (均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72,众数为75.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩 (均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72,众数为75.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com