
分析 (1)利用椭圆E的一个顶点为A(0,-1),焦点在x轴上,若椭圆右焦点到椭圆E的中心的距离是$\sqrt{2}$,求出椭圆的几何量,然后求解椭圆方程.
(2)先由原点O到直线l的距离为$\frac{\sqrt{3}}{2}$,求出k,再将直线l与椭圆联立,求出B、C坐标,转化求解三角形的面积即可.
解答 解:(1)椭圆E的一个顶点为A(0,-1),焦点在x轴上,若椭圆右焦点到椭圆E的中心的距离是$\sqrt{2}$
∴b=1,c=$\sqrt{2}$,则a=$\sqrt{3}$,
∴所求椭圆方程为$\frac{{x}^{2}}{3}$+y2=1.
(2)设C(x1,y1),B(x2,y2).由已知可得:$\frac{1}{\sqrt{1+{k}^{2}}}=\frac{\sqrt{3}}{2}$,
得k=$±\frac{\sqrt{3}}{3}$.不妨取k=$\frac{\sqrt{3}}{3}$.
又由$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x+1}\\{\frac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$,消去y得:
x2+$\sqrt{3}$x=0,∴x1=0,y1=1,x2=-$\sqrt{3}$,y2=0,∴|AB|=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2.
△BOC的面积:$\frac{1}{2}×2×1$=1.
当k=-$\frac{\sqrt{3}}{3}$时,所求三角形的面积也是1.
点评 本题考察了椭圆的标准方程,直线与椭圆相交的性质,解题时要特别注意韦达定理在解题中的重要应用,巧妙地运用设而不求的解题思想提高解题效率.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:选择题

| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=|2x-1|-2|x-1|.
已知函数f(x)=|2x-1|-2|x-1|.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
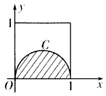 如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )| A. | 157 | B. | 314 | C. | 486 | D. | 628 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com