
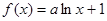
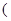
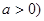 .
.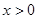 时,求证:
时,求证: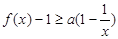 ;(4分)
;(4分)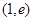 上
上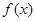
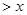 恒成立,求实数
恒成立,求实数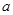 的范围。(4分)
的范围。(4分)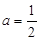 时,求证:
时,求证: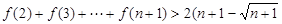 )
)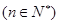 .(4分)
.(4分) 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
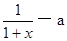 ,(f/(x))是f(x)的导数)
,(f/(x))是f(x)的导数)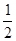
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为常数)
为常数) 上单调递增,且
上单调递增,且
 的图象在直线
的图象在直线
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
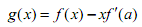 ,其中
,其中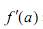 表示函数f(x)在
表示函数f(x)在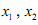 ,且
,且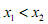 ,证明:
,证明: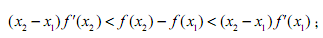
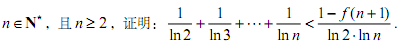
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
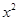 ,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;
,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;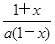 ,函数G(x)=h(x)·f(x),若对任意x∈(0,1),
,函数G(x)=h(x)·f(x),若对任意x∈(0,1),查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
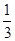 x3-(1+a)x2+4ax+24a,其中常数a>1.
x3-(1+a)x2+4ax+24a,其中常数a>1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com