
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 某商店的职工人数与商品销售额之间的相关系数为0.87 | |
| B. | 流通费用率与商业利润之间的相关系数为-0.94 | |
| C. | 商品销售额与商业利润之间的相关系数为0.51 | |
| D. | 商品销售额与流通费用率之间的相关系数为-0.81 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -4 | C. | -3 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
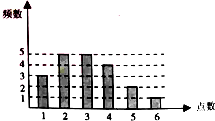 设有动点P,依次沿正方形ABCD的顶点A,B,C,D,A,B…移动,首先以A为出发点,根据一个骰子所掷出的点数移动P,掷出几点移动几步,其次以移动后多到达的点为出发点,再次进行同样的试验.
设有动点P,依次沿正方形ABCD的顶点A,B,C,D,A,B…移动,首先以A为出发点,根据一个骰子所掷出的点数移动P,掷出几点移动几步,其次以移动后多到达的点为出发点,再次进行同样的试验.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
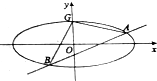 在平面直角坐标系xOy中,动点P到定点(1,0)的距离与到定直线x=2的距离之比为$\frac{\sqrt{2}}{2}$,设动点P的轨迹为C.
在平面直角坐标系xOy中,动点P到定点(1,0)的距离与到定直线x=2的距离之比为$\frac{\sqrt{2}}{2}$,设动点P的轨迹为C.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com