
【题目】已知过点![]() 的动直线
的动直线![]() 与圆
与圆![]() :
:![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 是
是![]() 中点,
中点,![]() 与直线
与直线![]() :
:![]() (
(![]() 为常数)相交于点
为常数)相交于点![]() .
.
(1)求证:当![]() 与
与![]() 垂直时,
垂直时,![]() 必过圆心
必过圆心![]() ;
;
(2)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)当直线![]() 的倾斜角
的倾斜角![]() 变化时,探索
变化时,探索![]() 的值是否为常数?若是,求出该常数;若不是,请说明理由.
的值是否为常数?若是,求出该常数;若不是,请说明理由.
【答案】(1)见解析;(2)![]() 或
或![]() ;(3)
;(3)![]() 为常数,该常数为
为常数,该常数为![]()
【解析】
(1)根据直线![]() 与
与![]() 垂直可得到直线
垂直可得到直线![]() 的斜率,由点斜式可得
的斜率,由点斜式可得![]() 的方程,由圆的方程可得圆心坐标,将圆心坐标代入直线
的方程,由圆的方程可得圆心坐标,将圆心坐标代入直线![]() 的方程满足可证结论正确,
的方程满足可证结论正确,
(2)利用弦长的一半,半径和勾股定理可求得![]() ,再讨论直线
,再讨论直线![]() 的斜率,利用点到直线的距离公式列等式可解得.
的斜率,利用点到直线的距离公式列等式可解得.
(3)利用![]() ,将
,将![]() 转化为
转化为![]() ,再讨论直线
,再讨论直线![]() 的斜率是否存在,可得点
的斜率是否存在,可得点![]() 的坐标,利用向量的数量积运算可得结论.
的坐标,利用向量的数量积运算可得结论.
如图所示:
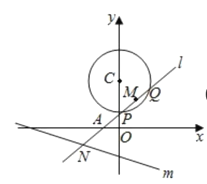
(1)证明: 当![]() 与
与![]() 垂直时,
垂直时,![]() ,所以直线
,所以直线![]() 的方程为:
的方程为:![]() ,即
,即![]() ,
,
又圆![]() :
:![]() 的圆心为
的圆心为![]() 满足直线
满足直线![]() 的方程,
的方程,
所以当![]() 与
与![]() 垂直时,
垂直时,![]() 必过圆心
必过圆心![]()
(2)因为圆![]() :
:![]() 的圆心
的圆心![]() ,半径为3,
,半径为3,
根据圆的性质可知,![]() ,所以有
,所以有![]() ,
,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 满足
满足![]() ,
,
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,即
,即![]() ,
,
由点到直线的距离可得![]()
![]() ,解得
,解得![]() ,
,
所以![]() ,即
,即![]() ,
,
综上所述:直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(3)因为![]() ,所以
,所以![]() ,
,
所以![]()
![]() ,
,
①当![]() 与
与![]() 轴垂直时,易得
轴垂直时,易得![]() ,
,
则![]() ,
,![]() ,
,
所以![]()
![]() ,
,
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
则由![]() 得
得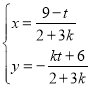 ,所以
,所以![]() ,
,
则![]() ,
,
所以![]()
![]()
![]()
![]()
![]() .
.
综上所述: ![]() 为常数,该常数为
为常数,该常数为![]() .
.


科目:高中数学 来源: 题型:
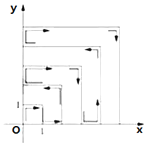
【题目】如图,一个粒子的起始位置为原点,在第一象限内于两正半轴上运动,第一秒运动到(0,1),而后它接着按图示在![]() 轴、
轴、![]() 轴的垂直方向来回运动,且每秒移动一个单位长度,如图所示,经过
轴的垂直方向来回运动,且每秒移动一个单位长度,如图所示,经过![]() 秒时移动的位置设为
秒时移动的位置设为![]() ,那么经过2019秒时,这个粒子所处的位置的坐标是______.
,那么经过2019秒时,这个粒子所处的位置的坐标是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业研制出一种型号为A的精密数控车床,A型车床为企业创造的价值逐年减少(以投产一年的年初到下一年的年初为A型车床所创造价值的第一年).若第 1 年A型车床创造的价值是250万元,且第1年至第6年,每年A型车床创造的价值减少30万元;从第7年开始,每年A型车床创造的价值是上一年价值的 50%.现用![]() (
(![]() )表示A型车床在第n年创造的价值.
)表示A型车床在第n年创造的价值.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)记![]() 为数列
为数列![]() 的前n项的和
的前n项的和![]()
![]() ,企业经过成本核算,若
,企业经过成本核算,若![]() 万元,则继续使用A型车床,否则更换A型车床,试问该企业须在第几年年初更换A型车床?(已知:若正数数列
万元,则继续使用A型车床,否则更换A型车床,试问该企业须在第几年年初更换A型车床?(已知:若正数数列![]() 是单调递减数列,则数列
是单调递减数列,则数列![]() 也是单调递减数列).
也是单调递减数列).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.

(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,求这
个,求这![]() 个芒果中恰有
个芒果中恰有![]() 个在
个在![]() 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所以芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京地铁八通线西起四惠站,东至土桥站,全长![]() ,共设13座车站
,共设13座车站![]() 目前八通线执行2014年12月28日制订的计价标准,各站间计程票价
目前八通线执行2014年12月28日制订的计价标准,各站间计程票价![]() 单位:元
单位:元![]() 如下:
如下:
四惠 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | |
四惠东 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | ||
高碑店 | 3 | span>3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | |||
传媒大学 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | ||||
双桥 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | |||||
管庄 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | ||||||
八里桥 | 3 | 3 | 3 | 3 | 4 | 4 | |||||||
通州北苑 | 3 | 3 | 3 | 3 | 3 | ||||||||
果园 | 3 | 3 | 3 | 3 | |||||||||
九棵树 | 3 | 3 | 3 | ||||||||||
梨园 | 3 | 3 | |||||||||||
临河里 | 3 | ||||||||||||
土桥 | |||||||||||||
四惠 | 四惠东 | 高碑店 | 传媒大学 | 双桥 | 管庄 | 八里桥 | 通州北苑 | 果园 | 九棵树 | 梨园 | 临河里 | 土桥 |
![]() 1
1![]() 在13座车站中任选两个不同的车站,求两站间票价为5元的概率;
在13座车站中任选两个不同的车站,求两站间票价为5元的概率;
![]() 2
2![]() 在土桥出站口随机调查了n名下车的乘客,将在八通线各站上车情况统计如下表:
在土桥出站口随机调查了n名下车的乘客,将在八通线各站上车情况统计如下表:
上车站点 | 通州北苑
| 双桥 | 四惠
|
频率 |
| a | b |
人数 | c | 15 | 25 |
求a,b,c,n的值,并计算这n名乘客乘车平均消费金额;
![]() 3
3![]() 某人从四惠站上车乘坐八通线到土桥站,中途任选一站出站一次,之后再从该站乘车
某人从四惠站上车乘坐八通线到土桥站,中途任选一站出站一次,之后再从该站乘车![]() 若想两次乘车花费总金额最少,可以选择中途哪站下车?
若想两次乘车花费总金额最少,可以选择中途哪站下车?![]() 写出一个即可
写出一个即可![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地种植常规稻A和杂交稻B,常规稻A的亩产稳定为500公斤,统计近年来数据得到每年常规稻A的单价比当年杂交稻B的单价高50%.统计杂交稻B的亩产数据,得到亩产的频率分布直方图如下;统计近10年来杂交稻B的单价(单位:元/公斤)与种植亩数(单位:万亩)的关系,得到的10组数据记为![]() ,并得到散点图如下,参考数据见下.
,并得到散点图如下,参考数据见下.
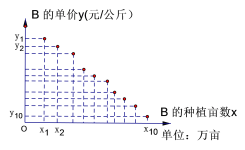
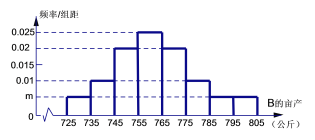
(1)求出频率分布直方图中m的值,若各组的取值按中间值来计算,求杂交稻B的亩产平均值;
(2)判断杂交稻B的单价y(单位:元/公斤)与种植亩数x(单位:万亩)是否线性相关,若相关,试根据以下统计的参考数据求出y关于x的线性回归方程;
(3)调查得到明年此地杂交稻B的种植亩数预计为2万亩,估计明年常规稻A的单价,若在常规稻A和杂交稻B中选择,明年种植哪种水稻收入更高?
统计参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
附:线性回归方程![]() ,
,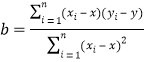 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②函数![]() ,的最小值是3
,的最小值是3
③用长为![]() 的铁丝围成--个平行四边形,则该平行四边形能够被直径为
的铁丝围成--个平行四边形,则该平行四边形能够被直径为![]() 的圆形纸片完全覆盖
的圆形纸片完全覆盖
④已知正实数![]() ,
,![]() 满足
满足![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
其中所有正确命题的序号是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com