
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源:不详 题型:填空题
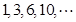 ,第
,第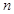 个三角形数为
个三角形数为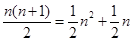 .记第
.记第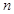 个
个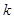 边形数为
边形数为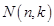 (
(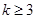 ),以下列出了部分
),以下列出了部分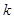 边形数中第
边形数中第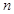 个数的表达式:
个数的表达式: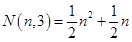 正方形数
正方形数 
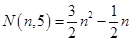 六边形数
六边形数 
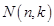 的表达式,由此计算
的表达式,由此计算 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.正确 | B.推理形式不正确 |
| C.两个“自然数”概念不一致 | D.两个“整数”概念不一致 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,用
,用 的四个数字由大到小重新排列成一个四位数m,再减去它的反序数n(即将
的四个数字由大到小重新排列成一个四位数m,再减去它的反序数n(即将 的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数
的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数 ,然后继续对
,然后继续对 重复上述变换,得数
重复上述变换,得数 ,…,如此进行下去,卡普耶卡发现,无论
,…,如此进行下去,卡普耶卡发现,无论 是多大的四位数,只要四个数字不全相同,最多进行k次上述变换,就会出现变换前后相同的四位数t(这个数称为Kaprekar变换的核).通过研究10进制四位数2014可得Kaprekar变换的核为 .
是多大的四位数,只要四个数字不全相同,最多进行k次上述变换,就会出现变换前后相同的四位数t(这个数称为Kaprekar变换的核).通过研究10进制四位数2014可得Kaprekar变换的核为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,则P点的轨迹为椭圆 |
| B.由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 |
C.由圆x2+y2=r2的面积πr2,猜想出椭圆 + + =1的面积S=πab =1的面积S=πab |
| D.以上均不正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com