
已知函数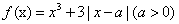 ,
,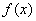 在
在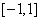 上的最小值记为
上的最小值记为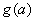 .(1)求
.(1)求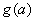 ;(2)证明:当
;(2)证明:当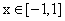 时,恒有
时,恒有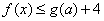 .
.
科目:高中数学 来源: 题型:
定义在R上的增函数y=f(x)对任意x,y∈R都有f(x+y)=f(x)+f(y).
(1)求f(0);
(2)求证:f(x)为奇函数;
(3)若f(k·3x)+f(3x-9x-2)<0对任意x∈R恒成立,求 实数k的取值范围.
实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
若直线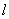 与曲线C满足下列两个条件:
与曲线C满足下列两个条件:
(i)直线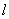 在点
在点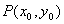 处与曲线C相切;(ii)曲线C在点
处与曲线C相切;(ii)曲线C在点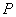 附近位于直线
附近位于直线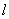 的两侧.则称直线
的两侧.则称直线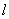 在点
在点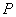 处“切过”曲线C.下列命题正确的是________(写出所有正确命题的编号).
处“切过”曲线C.下列命题正确的是________(写出所有正确命题的编号).
①直线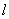 :y=0在点P(0,0)处“切过”曲线C
:y=0在点P(0,0)处“切过”曲线C :y=x3;
:y=x3;
②直线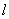 :x=-1在点P(-1,0)处“切过”曲线C:y=(x+1)2;
:x=-1在点P(-1,0)处“切过”曲线C:y=(x+1)2;
③直线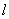 :y=x在点P(0,0)处“切过”曲线C:y=sin x;
:y=x在点P(0,0)处“切过”曲线C:y=sin x;
④直线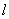 :y=x在点P(0,0)处“切过”曲线C:y=tan x;
:y=x在点P(0,0)处“切过”曲线C:y=tan x;
⑤直线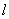 :y=x-1在点P(1,0)处“切过”曲线C:y=ln x.
:y=x-1在点P(1,0)处“切过”曲线C:y=ln x.
查看答案和解析>>
科目:高中数学 来源: 题型:
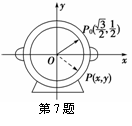
为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针针尖位置P(x,y).若初始位置为P0 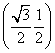 ,当秒针从P0(此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系式为________.
,当秒针从P0(此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系式为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
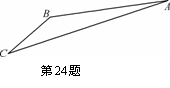
如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130 m/min,山路AC长为1 260 m,经测量,cosA=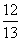 ,cosC=
,cosC=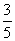 .
.
(1) 求索道AB的长;
(2) 问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3) 为使两位游客在C处互相等待的时间不超过3 min,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
已知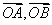 不共线,设
不共线,设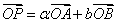 ,
,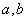 均为实数,且满足
均为实数,且满足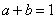 ,求证:
,求证: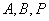 三点共线.
三点共线.
变式1:已知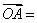 a + 2b,
a + 2b,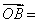 2a + 4b,
2a + 4b,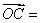 3a + 6b (其中a
3a + 6b (其中a  、b是两个任意非零向量) ,证明:A、B、C三点共线.
、b是两个任意非零向量) ,证明:A、B、C三点共线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com