
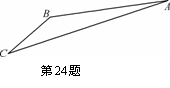
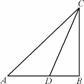
如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130 m/min,山路AC长为1 260 m,经测量,cosA=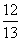 ,cosC=
,cosC=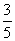 .
.
(1) 求索道AB的长;
(2) 问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3) 为使两位游客在C处互相等待的时间不超过3 min,乙步行的速度应控制在什么范围内?
(1) 在△ABC中,因为cosA=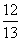 ,cosC=
,cosC=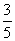 ,所以sinA=
,所以sinA=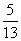 ,sinC=
,sinC=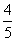 .
.
从而sinB=sin[π-(A+C)]=sin(A+C)=sinAcosC+cosAsi nC=
nC=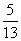 ×
×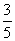 +
+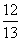 ×
×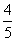 =
=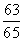 .
.
由正弦定理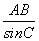 =
=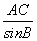 ,得AB=
,得AB=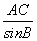 ×sinC=
×sinC=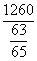 ×
×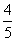 =1 040(m).
=1 040(m).
所以索道AB的长为1 040 m.
(2) 假设乙出发t min后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t m,所以由余弦定理得
d2=(100+50t)2+(130t)2-2×130t×(100+50t)×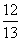 =200(37t2-70t+50),
=200(37t2-70t+50),
因0≤t≤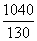 ,即0≤t≤8,故当t=
,即0≤t≤8,故当t=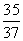 (min)时,甲、乙两游客距离最短.
(min)时,甲、乙两游客距离最短.
(3) 由正弦定理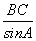 =
=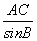 ,得BC=
,得BC=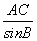 ×sinA=
×sinA=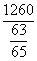 ×
×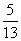 =500(m).
=500(m).
乙从B出发时,甲已走了50×(2+8+1)=550(m),还需走710 m才能到达C.设乙步行的速度为v m/min,由题意得-3≤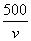 -
-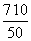 ≤3,解得
≤3,解得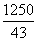 ≤v≤
≤v≤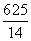 ,所以为使两位游客在C处互相等待的时间不超过3 min,乙步行的速度应控制在
,所以为使两位游客在C处互相等待的时间不超过3 min,乙步行的速度应控制在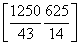 (单位:m/min)范围内.
(单位:m/min)范围内.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
将函数y=sin x的图象上所有的点向右平行移动 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是________________.
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
一人在海面某处测得某山顶C的仰角为α(0°<α<45°),在海面上向山顶的方向行进m 米后,测得山顶C的仰角为90°-α,则该山的高度为______米.(结果化简)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com