Question

17．填空：已知ABCD为一个平行四边形，对角线AC与BD相交于点O，则
$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{AC}$；$\overrightarrow{AB}$-$\overrightarrow{AD}$=$\overrightarrow{DB}$；
$\overrightarrow{BA}$-$\overrightarrow{BC}$=$\overrightarrow{CA}$；$\overrightarrow{BC}$-$\overrightarrow{BA}$=$\overrightarrow{AC}$；
$\overrightarrow{OA}$-$\overrightarrow{OB}$=$\overrightarrow{BA}$；$\overrightarrow{OD}$-$\overrightarrow{OA}$=$\overrightarrow{AD}$．

Answer 1

分析 根据向量加法的平行四边形法则及向量减法的几何意义即可对向量进行和或差的运算，从而求出答案．

解答 解：如图，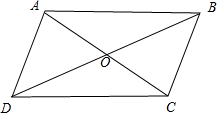

根据向量加法的平行四边形法则及向量减法的几何意义得：
$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$$，\overrightarrow{BA}-\overrightarrow{BC}=\overrightarrow{CA}$，$\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}$，$\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DB}$，$\overrightarrow{BC}-\overrightarrow{BA}=\overrightarrow{AC}$，$\overrightarrow{OD}-\overrightarrow{OA}=\overrightarrow{AD}$．
故答案为：$\overrightarrow{AC}，\overrightarrow{CA}，\overrightarrow{BA}，\overrightarrow{DB}，\overrightarrow{AC}，\overrightarrow{AD}$．

点评 考查向量加法的平行四边形法则，以及向量的减法的几何意义．