练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．某单位共有163人，其中老年人27人，中年人55人，青年人81人，为了调查他们的身体状况，需要从他们中抽取一个容量为36的样本，问应当采用怎样的抽样方法？中年人应抽查多少人？

    分析 由于各部分之间的身体状况有较大差别，故应当采用怎样分层抽样方法，样本才具有可行性．三部分的人数不成比例，应从中年人中随机剔除1人，得：27：54：81=1：2：3，由此能求出中年人应抽查的人数．

    解答 解：∵某单位共有163人，其中老年人27人，中年人55人，青年人81人，
    为了调查他们的身体状况，需要从他们中抽取一个容量为36的样本，
    由于各部分之间的身体状况有较大差别，
    ∴应当采用怎样分层抽样方法，样本才具有可行性．
    ∵三部分的人数不成比例，∴应从中年人中随机剔除1人，得：27：54：81=1：2：3，
    ∴将36人分成1：2：3的三部分，
    设三部分各抽取个体数分别为：x，2x，3x，
    则x+2x+3x=36，解得x=6，∴2x=12．
    故中年人应抽查12人．

    点评 本题考查抽查的样本个数的求法，是基础题，解题时要认真审题，注意分层抽样的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    14．已知数列{an}满足a1=81，an=$\left\{\begin{array}{l}-1+{log_3}{a_{n-1}}，\;n=2k\\{3^{{a_{n-1}}}}，n=2k+1\end{array}$（k∈N*），则数列{an}的前n项和Sn的最大值为127．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知i是虚数单位，若z1=a+$\frac{\sqrt{3}}{2}$i，z2=a-$\frac{\sqrt{3}}{2}$i，若$\frac{{z}_{1}}{{z}_{2}}$为纯虚数，则实数a=±$\frac{\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知等比数列{an}满足a1=1，a4=4（a3-a2），数列{bn}满足bn=1+2log2an．
    （1）求数列{an}和{bn}的通项公式；
    （2）令Tn=$\frac{{b}_{1}}{{a}_{n}}$+$\frac{{b}_{2}}{{a}_{n-1}}$+$\frac{{b}_{3}}{{a}_{n-2}}$…+$\frac{{b}_{n-1}}{{a}_{2}}$+$\frac{{b}_{n}}{{a}_{1}}$，求Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．△ABC的内角A，B，C所对的边分别为a，b，c，已知1+$\frac{tanA}{tanB}$=$\frac{2c}{b}$．
    （I）求A；
    （Ⅱ）若BC边上的中线AM=2$\sqrt{2}$，高线AH=$\sqrt{3}$，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．从某校的一次学料知识竞赛成绩中，随机抽取了50名同学的成绩，统计如下：
     组别[30，40][40，50][50，60][60，70][70，80][80，90][90，100]
     频数 3 10 12 15 6 2 2
    （Ⅰ）求这50名同学成绩的样本平均数$\overline{x}$（同一组中的数据用该组区间的中点值作代表）；
    （Ⅱ）由频数分布表可以认为，本次学科知识竞赛的成绩Z服从正态分布N（μ，196），其中μ近似为样本平均数$\overline{x}$．
    ①利用该正态分布．求P（Z＞74）；
    ②某班级共有20名同学参加此次学科知识比赛，记X表示这20名同学中成绩超过74分的人数，利用①的结果，求EX．附：若Z～N（μ，σ2），则P（μ-σ＜Z＜+σ）=0.6826，P（μ-2＜Z＜μ+2σ）=0.9544．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

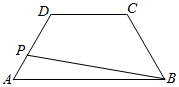    16．如图，在等腰梯形ABCD中，AB=8，BC=4，CD=4，点P在线段AD上运动，则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围是（　　）
    A．[6，4+4$\sqrt{3}$]B．[4$\sqrt{2}$，8]C．[4$\sqrt{3}$，8]D．[6，12]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知函数f（x）=$\frac{x-2}{x+2}$，则f（0）=（　　）
    A．0B．1C．2D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知双曲线C的渐近线方程为3x±2y=0，且焦点在x轴上，焦点到渐近线的距离为6，则该双曲线的方程为（　　）
    A．$\frac{x^2}{18}-\frac{y^2}{8}=1$B．$\frac{x^2}{36}-\frac{y^2}{16}=1$C．$\frac{x^2}{8}-\frac{y^2}{18}=1$D．$\frac{x^2}{16}-\frac{y^2}{36}=1$

    查看答案和解析>>

    同步练习册答案