
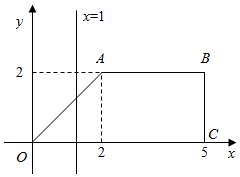
 如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).
如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).分析 (1)分情况讨论:当0≤t≤2时,所求面积等于四边形OABC的面积减去一三角形面积;当2<t≤5时,所求面积等于一矩形面积.
(2)根据各段函数表达式的特征分别画出即可.
解答 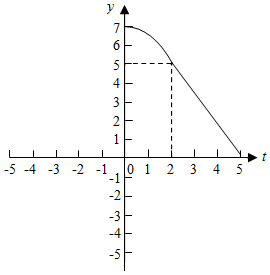 (1)设直线x=t与x轴交于点D,与线段OA交于点E,与线段AB交于点F,
(1)设直线x=t与x轴交于点D,与线段OA交于点E,与线段AB交于点F,
则SOCBA=$\frac{1}{2}$×2×2+(5-2)×2=8,
①当0≤t≤2时,f(t)=S0CBS-S△ODE=8-$\frac{1}{2}$t2,
②当2<t≤5时,f(t)=SDCBF=(5-t)×2=10-2t,
所以f(t)=$\left\{\begin{array}{l}{8-\frac{1}{2}{t}^{2}(0≤t≤2)}\\{10-2t(2<t≤5)}\end{array}\right.$.
(2)y=f(t)的图象如图所示:
点评 本题考查函数解析式的求法及简单函数的图象,注意分类讨论思想在本题中的运用.


科目:高中数学 来源: 题型:填空题
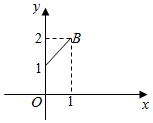 设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图所示的线段AB,则方程[f(x)]2=x的最大实数根的值为$\frac{11-\sqrt{21}}{2}$.
设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图所示的线段AB,则方程[f(x)]2=x的最大实数根的值为$\frac{11-\sqrt{21}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x-1与g(x)=$\sqrt{{x}^{2}-2x+1}$ | B. | f(x)=x与g(x)=$\frac{{x}^{2}}{x}$ | ||
| C. | f(x)=x与g(x)=$\root{3}{x^3}$ | D. | f(x)=$\frac{{x}^{2}-4}{x-2}$与g(x)=x+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 6或-6 | C. | 1或-6 | D. | 6或-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com