
分析 设MN:x-y+c=0(-$\frac{1}{2}$<c<1),求出P到MN的距离,|MN|,可得三角形的面积,再用导数法求解即可.
解答 解:设MN:x-y+c=0(-$\frac{1}{2}$<c<1),则P到MN的距离为$\frac{|c-1|}{\sqrt{2}}$,
x-y+c=0与x2=2y联立,可得x2-2x-2c=0,∴x=1±$\sqrt{2c+1}$,
∴|MN|=$\sqrt{2}•$2$\sqrt{2c+1}$,
∴△PMN的面积=$\frac{1}{2}$•$\sqrt{2}•$2$\sqrt{2c+1}$•$\frac{|c-1|}{\sqrt{2}}$=$\sqrt{(2c+1)(c-1)^{2}}$
令y=(2c+1)(c-1)2,∴y′=6c(c-1)
∴(-$\frac{1}{2}$,0),y′>0,(0,1)上,y′<0
∴c=0时,y取得最大值1,
∴△PMN的面积的最大值为1.
故答案为:1.
点评 本题考查三角形面积的计算,考查直线与抛物线的位置关系,考查导数知识的运用,确定三角形的面积是关键.


科目:高中数学 来源: 题型:选择题
| A. | 0<b<a<1 | B. | 0<a<b<1 | C. | a>b>1 | D. | 0<a<1<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | [2,3) | C. | (2,3) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x≥0,|x0|+x0<0 | B. | ?x<0,|x|+x≥0 | C. | ?x0≥0,|x0|+x0<0 | D. | ?x0<0,|x|+x≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
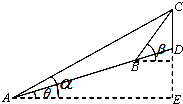 如图,一山顶有一信号塔CD(CD所在的直线与地平面垂直),在山脚A处测得塔尖C的仰角为α,沿倾斜角为θ的山坡向上前进l米后到达B处,测得C的仰角为β.
如图,一山顶有一信号塔CD(CD所在的直线与地平面垂直),在山脚A处测得塔尖C的仰角为α,沿倾斜角为θ的山坡向上前进l米后到达B处,测得C的仰角为β.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com