
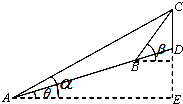
 如图,一山顶有一信号塔CD(CD所在的直线与地平面垂直),在山脚A处测得塔尖C的仰角为α,沿倾斜角为θ的山坡向上前进l米后到达B处,测得C的仰角为β.
如图,一山顶有一信号塔CD(CD所在的直线与地平面垂直),在山脚A处测得塔尖C的仰角为α,沿倾斜角为θ的山坡向上前进l米后到达B处,测得C的仰角为β.分析 (1)直接利用正弦定理列出关系式即可.
(2)通过关系式,利用正弦定理化简求解即可.
解答 (本小题满分12分)
解:(1)在△ABC中,∠CAB=α-θ,∠ABC=π-(β-θ),∠ACB=β-α,
由正弦定理,$BC=\frac{sin(α-θ)}{sin(β-α)}l$.(6分)
(2)由(1)及条件知,$BC=\frac{sin(α-θ)}{sin(β-α)}l=12(\sqrt{6}-\sqrt{2})$,∠BCD=90°-β=15°,∠CBD=β-θ=45°,∠BDC=120°,由正弦定理得,$CD=\frac{sin45°}{sin120°}•BC=24-8\sqrt{3}$.
(12分)
点评 本小题主要考查利用解三角形的思想解决实际问题,对考生的抽象概括能力和运算求解能力,化归与转化能力提出一定要求.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是
如图,已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com