Question

9．△ABC的外接圆圆心为O，半径为2，$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow 0$，且|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|，$\overrightarrow{CA}$在$\overrightarrow{CB}$方向上的投影为（　　）

• A． -3
• B． -$\sqrt{3}$
• C． $\sqrt{3}$
• D． 3

Answer 1

分析 由题意，得到四边形OCAB是边长为2的菱形，$\overrightarrow{CA}$在$\overrightarrow{CB}$方向上的投影为对角线BC的一半．

解答 解：由题意，$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow 0$，得到$\overrightarrow{OB}+\overrightarrow{AC}=\overrightarrow{0}$，又|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|=|$\overrightarrow{OB}$|，△OAB是等边三角形，所以四边形OCAB是边长为2的菱形，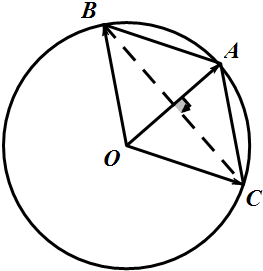
所以$\overrightarrow{CA}$在$\overrightarrow{CB}$方向上的投影为ACcos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$；
故选C．

点评 本题考查了向量的投影；解得本题的关键是由题意，画出图形，明确四边形OBAC的形状，利用向量解答．