
 如图,已知在等腰梯形ABCD中,AB=4,AB∥CD,∠BAD=45°,E,F,G分别是AB,BC,CD的中点,若$\overrightarrow{EF}$在$\overrightarrow{AG}$方向上的投影为$\frac{7}{10}\sqrt{4+\frac{1}{2}A{D^2}}$,则$\frac{{|\overrightarrow{AB}|}}{{|\overrightarrow{CD}|}}$=( )
如图,已知在等腰梯形ABCD中,AB=4,AB∥CD,∠BAD=45°,E,F,G分别是AB,BC,CD的中点,若$\overrightarrow{EF}$在$\overrightarrow{AG}$方向上的投影为$\frac{7}{10}\sqrt{4+\frac{1}{2}A{D^2}}$,则$\frac{{|\overrightarrow{AB}|}}{{|\overrightarrow{CD}|}}$=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由题意建立平面直角坐标系,从而利用平面向量的坐标表示化简即可.
解答 解:建立如右图所示的平面直角坐标系,
∵,∠BAD=45°,∴设D(x,x),(x>0),
则C(4-x,x),G(2,x),E(2,0),F($\frac{8-x}{2}$,$\frac{x}{2}$),
故$\overrightarrow{EF}$=(2-$\frac{x}{2}$,$\frac{x}{2}$),
所以$\overrightarrow{EF}$在$\overrightarrow{AG}$方向上的投影为
$\frac{\overrightarrow{EF}•\overrightarrow{AG}}{|\overrightarrow{AG}|}$=$\frac{2(2-\frac{x}{2})+x\frac{x}{2}}{\sqrt{4+{x}^{2}}}$=$\frac{7}{10}\sqrt{4+\frac{1}{2}A{D^2}}$,
即$\frac{2(2-\frac{x}{2})+x\frac{x}{2}}{\sqrt{4+{x}^{2}}}$=$\frac{7}{10}$$\sqrt{4+\frac{1}{2}({x}^{2}+{x}^{2})}$,
解得,x=1;
故CD=4-2=2,
故$\frac{{|\overrightarrow{AB}|}}{{|\overrightarrow{CD}|}}$=2,
故选:B.
点评 本题考查了平面向量的坐标运算、平面向量的投影等基础知识,同时考查了坐标法、方程思想的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
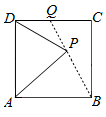 如图,在边长为2的正方形ABCD中,点Q边CD上一个动点,$\overrightarrow{CQ}$=λ$\overrightarrow{QD}$,点P为线段BQ(含端点)上一个动点,若λ=1,则$\overrightarrow{PA}$•$\overrightarrow{PD}$的取值范围为[$\frac{4}{5}$,4].
如图,在边长为2的正方形ABCD中,点Q边CD上一个动点,$\overrightarrow{CQ}$=λ$\overrightarrow{QD}$,点P为线段BQ(含端点)上一个动点,若λ=1,则$\overrightarrow{PA}$•$\overrightarrow{PD}$的取值范围为[$\frac{4}{5}$,4].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com