
分析 (1)利用余弦定理列方程解出;
(2)根据正弦定理用θ表示出BN,BM,使用和角公式化简L,根据θ的范围和正弦函数的性质得出L的最大值.
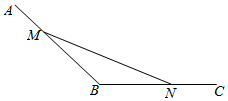
解答 解:(1)设BM=x,则BN=x-4,MN=x+4,
在△MBN中,由余弦定理得MN2=BN2+BM2-2BN•BMcosB,
即(x+4)2=(x-4)2+x2+x(x-4),解得x=10,
∴MN=x+4=14(千米);
(2)∠BMN=60°-θ,
由正弦定理得$\frac{BM}{sinθ}$=$\frac{BN}{sin(60°-θ)}$=$\frac{MN}{sin120°}$=8$\sqrt{3}$,
∴BM=8$\sqrt{3}$sinθ,BN=8$\sqrt{3}$sin(60°-θ),
∴L=BM+BN+MN=8$\sqrt{3}$sinθ+8$\sqrt{3}$sin(60°-θ)+12=12cosθ+4$\sqrt{3}$sinθ+12=8$\sqrt{3}$sin(θ+60°)+12.
∵0<θ<60°,∴60°<θ+60°<120°.
∴当θ+60°=90°时,周长L取得最大值8$\sqrt{3}$+12千米.
点评 本题考查了正余弦定理在解三角形中的应用,三角函数的恒等变换,正弦函数的图象与性质,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
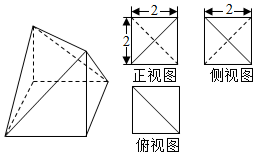 已知某几何体的直观图及三视图如图所示,三视图的轮廓均为正方形,则该几何体的表面积为( )
已知某几何体的直观图及三视图如图所示,三视图的轮廓均为正方形,则该几何体的表面积为( )| A. | 14+2$\sqrt{3}$ | B. | 12+4$\sqrt{3}$ | C. | 16+4$\sqrt{3}$ | D. | 15+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x+$\frac{4}{x}$ | B. | y=sinx+$\frac{4}{sinx}$(0<x<π) | ||
| C. | y=ex+4e-x | D. | y=$\sqrt{{x}^{2}+3}$+$\frac{2}{\sqrt{{x}^{2}+3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正方体ABCD-A1B1C1D1中,E为线段B1C的中点,若三棱锥E-ADD1外接球的体积为36π,则正方体的棱长为( )
如图,正方体ABCD-A1B1C1D1中,E为线段B1C的中点,若三棱锥E-ADD1外接球的体积为36π,则正方体的棱长为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com