
分析 把数列递推式变形,可得数列数列{$\frac{1}{{a}_{n}}$-$\frac{1}{2}$}是以$\frac{3}{2}$为首项,以$\frac{1}{3}$为公比的等比数列,求出等比数列的通项公式后可得an.
解答 解:∵f(x)=$\frac{3x}{x+1}$,数列满足an+1=f(an),
∴an+1=$\frac{3{a}_{n}}{{a}_{n}+1}$,
∴$\frac{1}{{a}_{n+1}}$=$\frac{{a}_{n}+1}{3{a}_{n}}$,
∴$\frac{1}{{a}_{n+1}}$=$\frac{{a}_{n}+1}{3{a}_{n}}$=$\frac{1}{3}$+$\frac{1}{3{a}_{n}}$,
即$\frac{1}{{a}_{n+1}}$-$\frac{1}{2}$=$\frac{1}{3}$($\frac{1}{{a}_{n}}$-$\frac{1}{2}$),
∵a1=$\frac{1}{2}$,
∴$\frac{1}{{a}_{1}}$-$\frac{1}{2}$=$\frac{3}{2}$,
∴数列{$\frac{1}{{a}_{n}}$-$\frac{1}{2}$}是以$\frac{3}{2}$为首项,以$\frac{1}{3}$为公比的等比数列,
∴$\frac{1}{{a}_{n}}$-$\frac{1}{2}$=$\frac{3}{2}$($\frac{1}{3}$)n-1,
∴$\frac{1}{{a}_{n}}$=$\frac{1}{2}$+$\frac{3}{2}$($\frac{1}{3}$)n-1,
∴an=$\frac{2×{3}^{n-1}}{3+{3}^{n-1}}$,n∈N+.
点评 本题考查数列递推式,考查了等比关系的确定,是中档题.


科目:高中数学 来源: 题型:解答题
| 专业 性别 | 中文 | 英语 | 数学 | 体育 |
| 男 | m | 1 | n | 1 |
| 女 | 1 | 1 | 1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3n | B. | $\frac{2}{{3}^{n}}$ | C. | $\frac{1}{{3}^{n}}$ | D. | 3n-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
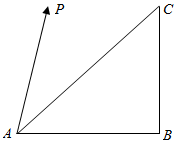 等腰直角△ABC的直角顶点为B,两条直角边长都为1,点P为三角形所在平面内的一点,若$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+$μ\overrightarrow{AC}$,且|$\overrightarrow{AP}$|=1,则λ的取值范围为( )
等腰直角△ABC的直角顶点为B,两条直角边长都为1,点P为三角形所在平面内的一点,若$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+$μ\overrightarrow{AC}$,且|$\overrightarrow{AP}$|=1,则λ的取值范围为( )| A. | [-1,$\sqrt{2}$] | B. | [-$\sqrt{2}$,$\sqrt{2}$] | C. | [-$\sqrt{2}$,1] | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\sqrt{2}$-1 | C. | 1 | D. | $\frac{\sqrt{2}+1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com