
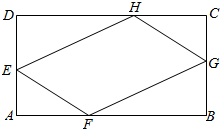
 如图,在矩形ABCD中,已知AD=1.5,AB=a(a>1.5),E,F,G,H分别是边AD,AB,BC,CD上的动点,且满足AE=AF=CG=CH.若AE=x,当x变化时.
如图,在矩形ABCD中,已知AD=1.5,AB=a(a>1.5),E,F,G,H分别是边AD,AB,BC,CD上的动点,且满足AE=AF=CG=CH.若AE=x,当x变化时.分析 (1)设AE=x,四边形EFGH的面积为S,则S=1.5a-x2-(1.5-x)(a-x),x∈(0,1.5].
(2)化简并配方,可得函数的对称轴,从而分类讨论区间和对称轴的关系,可求函数的最大值.
解答 解:设AE=x,四边形EFGH的面积为S,
则S=1.5a-x2-(1.5-x)(a-x)
=-2x2+(a+1.5)x
=-2(x-$\frac{a+1.5}{4}$)2+$\frac{(a+1.5)^{2}}{8}$,x∈(0,1.5],
(1)若$\frac{a+1.5}{4}$≤1.5,即1.5<a≤4.5,
则当x=$\frac{a+1.5}{4}$时,S取得最大值是Smax=$\frac{(a+1.5)^{2}}{8}$;
(2)若$\frac{a+1.5}{4}$>1.5,即a>4.5,
函数S=-2x2+(a+1.5)x在区间(0,1.5]上是增函数,
则当x=1.5时,S取得最大值是Smax=1.5a-2,25.
综上可得EFGH的面积的最大值为$\left\{\begin{array}{l}{\frac{(a+1.5)^{2}}{8},1.5<a≤4.5}\\{1.5a-2.25,a>4.5}\end{array}\right.$.
点评 本题以实际问题为载体,考查二次函数模型的构建,考查二次函数在闭区间上的最值讨论,解题的关键是针对函数的定义域,结合函数的对称轴分类讨论.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1lnx2<x2lnx1 | B. | x1lnx2>x2lnx1 | ||
| C. | x1e${\;}^{{x}_{2}}$<x2e${\;}^{{x}_{1}}$ | D. | x1e${\;}^{{x}_{2}}$>x2e${\;}^{{x}_{1}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com