
已知 ,函数
,函数 .
.
(1) 时,写出
时,写出 的增区间;
的增区间;
(2)记 在区间[0,6]上的最大值为
在区间[0,6]上的最大值为 ,求
,求 的表达式;
的表达式;
(3)是否存在 ,使函数
,使函数 在区间(0,6)内的图象上存在两点,在该两点处的切线互相垂直?若存在,求
在区间(0,6)内的图象上存在两点,在该两点处的切线互相垂直?若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(1)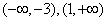 ;
;
(2)当0≤x≤t时,f(x)=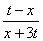 ;当x>t时,f(x)=
;当x>t时,f(x)=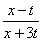 .
.
因此,当x∈(0,t)时,f′(x)=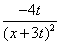 <0,f(x)在(0,t)上单调递减;
<0,f(x)在(0,t)上单调递减;
当x∈(t,+∞)时,f′(x)= >0,f(x)在(t,+∞)上单调递增.
>0,f(x)在(t,+∞)上单调递增.
①若t≥6,则f(x)在(0,6)上单调递减,g(t)=f(0)=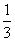 .
.
②若0<t<6,则f(x)在(0,t)上单调递减,在(t,6)上单调递增.
所以g(t)=mtx{f(0),f(6)}.
而f(0)-f(6)=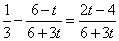 ,故当0<t≤2时,g(t)=f(6)=
,故当0<t≤2时,g(t)=f(6)=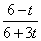 ;
;
当2<t<6时,g(t)=f(0)=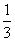 .综上所述,g(t)=
.综上所述,g(t)=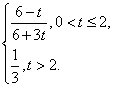
(3)由(1)知,当t≥6时,f(x)在(0,6)上单调递减,故不满足要求.
当0<t<6时,f(x)在(0,t)上单调递减,在(t,6)上单调递增.
若存在x1,x2∈(0,6)(x1<x2),使曲线y=f(x)在(x1,f(x1)),(x2,f(x2))两点处的切线互相垂直,则x1∈(0,t),x2∈(t,6),且f′(x1)·f′(x2)=-1,
即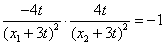 .亦即x1+3t=
.亦即x1+3t=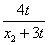 .(*)
.(*)
由x1∈(0,t),x2∈(t,6)得x1+3t∈(3t,4t),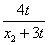 ∈
∈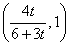 .
.
故(*)成立等价于集合T={x|3t<x<4t}与集合B=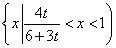 的交集非空.因为
的交集非空.因为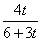 <4t,所以当且仅当0<3t<1,即0<t<
<4t,所以当且仅当0<3t<1,即0<t<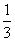 时,T∩B≠
时,T∩B≠ .
.
综上所述,存在t使函数f(x)在区间(0,6)内的图象上存在两点,在该两点处的切线互相垂直,且t的取值范围是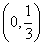 .
.


科目:高中数学 来源: 题型:
已知直线 和双曲线
和双曲线 相交于A,B两点,线段AB的中点为M.设直线
相交于A,B两点,线段AB的中点为M.设直线 的斜率为k1(k1≠0),直线OM的斜率为k2,则k1k2=( )
的斜率为k1(k1≠0),直线OM的斜率为k2,则k1k2=( )
A.  B. -
B. - C. -
C. - D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
一个四面体的四个顶点在空间直角坐标系 中的坐标分别是(0,0,0),(1,2,0),(0,2,2),(3,0,1),则该四面体中以
中的坐标分别是(0,0,0),(1,2,0),(0,2,2),(3,0,1),则该四面体中以 平面为投影面的正视图的面积为
平面为投影面的正视图的面积为
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
复数 的共轭复数是a+bi(a,b∈R),i是虛数单位,则点(a,b)为( )
的共轭复数是a+bi(a,b∈R),i是虛数单位,则点(a,b)为( )
|
| A. | (1,2) | B. | (2,﹣i) | C. | (2,1) | D. | (1,﹣2) |
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,角A、B、C的对边分别为a、b、c,如果cos(2B+C)+2sinAsinB<0,那么三边长a、b、c之间满足的关系是( )
|
| A. | 2ab>c2 | B. | a2+b2<c2 | C. | 2bc>a2 | D. | b2+c2<a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点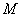 是椭圆
是椭圆 :
: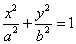
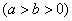 上一点,
上一点,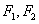 分别为
分别为 的左右焦点,
的左右焦点,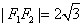 ,
,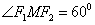 ,
,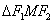 的面积为
的面积为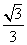 .
.
(1)求椭圆 的方程;
的方程;
(2)设过椭圆右焦点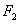 的直线
的直线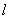 和椭圆交于两点
和椭圆交于两点 ,是否存在直线
,是否存在直线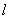 ,使得△
,使得△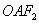 与
与
△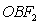 的面积比值为
的面积比值为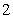 ?若存在,求出直线
?若存在,求出直线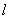 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com