
【题目】已知圆C:x2+y2﹣6x﹣8y﹣5t=0,直线l:x+3y+15=0.
(1)若直线l被圆C截得的弦长为 ![]() ,求实数t的值;
,求实数t的值;
(2)当t=1时,由直线l上的动点P引圆C的两条切线,若切点分别为A,B,则在直线AB上是否存在一个定点?若存在,求出该定点的坐标;若不存在,请说明理由.
【答案】
(1)解:圆C的方程可化为(x﹣3)2+(y﹣4)2=25+5t
故圆心为C(3,4),半径 ![]()
则圆心C到直线l的距离为 ![]()
又弦长为 ![]() ,则
,则 ![]() 即
即 ![]() ,解得t=15
,解得t=15
(2)解:当t=1时,圆C的方程为x2+y2﹣6x﹣8y﹣5=0①
则圆心为C(3,4),半径 ![]() ,圆C与直线l相离假设在直线AB上存在一个定点满足条件,设动点P(m,n)
,圆C与直线l相离假设在直线AB上存在一个定点满足条件,设动点P(m,n)
由已知得PA⊥AC,PB⊥BC
则A,B在以CP为直径的圆(x﹣3)(x﹣m)+(y﹣4)(y﹣n)=0
即x2+y2﹣(3+m)x﹣(4+n)y+3m+4n=0上②
①﹣②得,直线AB的方程为(m﹣3)x+(n﹣4)y﹣3m﹣4n﹣5=0③
又点P(m,n)在直线l上,则m+3n+15=0,即m=﹣3n﹣15,代入③式
得(﹣3n﹣18)x+(n﹣4)y+9n+45﹣4n﹣5=0
即直线AB的方程为18x+4y﹣40+n(3x﹣y﹣5)=0
因为上式对任意n都成立,故 ![]() ,得
,得 ![]()
故在直线AB上存在一个定点,定点坐标为(2,1)
【解析】(1)根据直线和圆相交,利用弦长公式进行求解即可.(2)利用直线和圆相切的条件,建立方程关系进行求解判断.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】从某校高三学生中随机抽取了![]() 名学生,统计了期末数学考试成绩如下表:
名学生,统计了期末数学考试成绩如下表:
(1)请在频率分布表中的①、②位置上填上相应的数据,并在给定的坐标系中作出这些数据的频率分布直方图,再根据频率分布直方图估计这![]() 名学生的平均成绩;
名学生的平均成绩;
(2)用分层抽样的方法在分数在![]() 内的学生中抽取一个容量为
内的学生中抽取一个容量为![]() 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取![]() 人,求至少有
人,求至少有![]() 人的分数在
人的分数在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2cos2x,
=(2cos2x, ![]() ),
), ![]() =(1,sin2x),函数f(x)=
=(1,sin2x),函数f(x)= ![]()
![]() ﹣1.
﹣1.
(1)当x= ![]() 时,求|a﹣b|的值;
时,求|a﹣b|的值;
(2)求函数f(x)的最小正周期以及单调递增区间;
(3)求方程f(x)=k,(0<k<2),在[﹣ ![]() ,
, ![]() ]内的所有实数根之和.
]内的所有实数根之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为C的圆经过点A(0,2)和B(1,1),且圆心C在直线l:x+y+5=0上.
(1)求圆C的标准方程;
(2)若P(x,y)是圆C上的动点,求3x﹣4y的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】刘徽是我国魏晋时期著名的数学家,他编著的《海岛算经》中有一问题:“今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从后表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高几何?” 意思是:为了测量海岛高度,立了两根表,高均为5步,前后相距1000步,令后表与前表在同一直线上,从前表退行123步,人恰观测到岛峰,从后表退行127步,也恰观测到岛峰,则岛峰的高度为( )(注:3丈=5步,1里=300步)
A. 4里55步 B. 3里125步 C. 7里125步 D. 6里55步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.有两个面平行,其余各面都是四边形的几何体叫棱柱.
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱.
C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥.
D.棱台各侧棱的延长线交于一点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是为求S=1+ ![]() +
+ ![]() +…
+… ![]() 的和而设计的程序框图,将空白处补上,指明它是循环结构中的哪一种类型,并画出它的另一种循环结构框图.如图是当型循环结构.
的和而设计的程序框图,将空白处补上,指明它是循环结构中的哪一种类型,并画出它的另一种循环结构框图.如图是当型循环结构.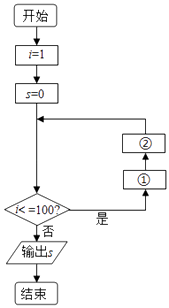
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com