
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知函数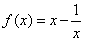
(1)判断函数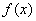 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)用定义证明函数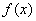 在区间
在区间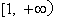 上为增函数;
上为增函数;
(3)若函数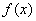 在区间
在区间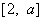 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于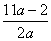 ,求
,求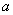 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆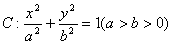 的离心率为
的离心率为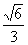 ,
,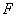 为椭圆在
为椭圆在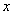 轴正半轴上的焦点,
轴正半轴上的焦点,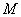 、
、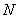 两点在椭圆
两点在椭圆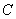 上,且
上,且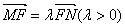 ,定点
,定点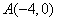 .
.
(I)求证:当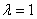 时
时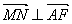 ;
;
(II)若当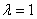 时有
时有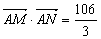 ,求椭圆
,求椭圆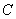 的方程;
的方程;
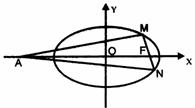 (III)在(II)的椭圆中,当
(III)在(II)的椭圆中,当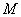 、
、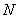 两点在椭圆
两点在椭圆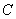 上运动时,试判断
上运动时,试判断 是否有最大值,若存在,求出最大值,并求出这时
是否有最大值,若存在,求出最大值,并求出这时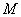 、
、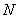 两点所在直线方程,若不存在,给出理由.
两点所在直线方程,若不存在,给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面几何里,有勾股定理:“设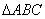 的两边AB、AC互相垂直,则
的两边AB、AC互相垂直,则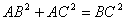 。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com