
在平面几何里,有勾股定理:“设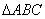 的两边AB、AC互相垂直,则
的两边AB、AC互相垂直,则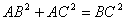 。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
科目:高中数学 来源: 题型:
在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则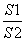 =
=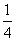 ,推广到空间可以得到类似结论;已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则
,推广到空间可以得到类似结论;已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则 =( )
=( )
A.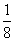 B.
B.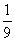 C.
C. D.
D.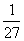
查看答案和解析>>
科目:高中数学 来源: 题型:
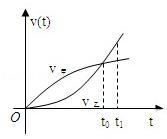
已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V已(如图所示).那么对于图中给定的t0和t1,下列判断中一定正确的是( )
A.在t1时刻,甲车在乙车前面 B.t1时刻后,甲车在乙车后面
C.在t0时刻,两车的位置相同 D.t0时刻后,乙车在甲车前面
查看答案和解析>>
科目:高中数学 来源: 题型:
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为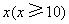 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为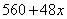 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用 平均建筑费用
平均建筑费用 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
袋中有大小相同的编号为1到8的球各一只,自袋中随机取出两球,设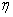 为取出两球中的较小编号,若
为取出两球中的较小编号,若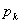 表示
表示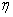 取值为
取值为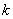
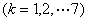 的概率,则满足
的概率,则满足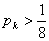 的
的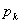 个数是( ).
个数是( ).
A. 5 B. 4 C . 3 D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
下列四个说法:
①一个命题的逆命题为真,则它的逆否命题一定为真;
②命题“设a,b∈R,若a+b≠6,则a≠3或b≠3”是一个假命题;
③“x>2”是“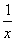 <
<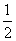 ”的充分不必要条件;
”的充分不必要条件;
④一个命题的否命题为真,则它的逆命题一定为真.
其中说法不正确的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com