
袋中有大小相同的编号为1到8的球各一只,自袋中随机取出两球,设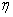 为取出两球中的较小编号,若
为取出两球中的较小编号,若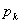 表示
表示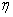 取值为
取值为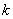
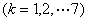 的概率,则满足
的概率,则满足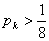 的
的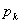 个数是( ).
个数是( ).
A. 5 B. 4 C . 3 D. 2
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
设数列{an}的前n项和为Sn,且方程x2-anx-an=0有一根为Sn-1,n=1,2,3…….
(1)求a1,a2;
(2)猜想数列{Sn}的通项公式,并给出严格的证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面几何里,有勾股定理:“设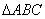 的两边AB、AC互相垂直,则
的两边AB、AC互相垂直,则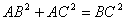 。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列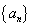 中,
中,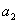 =
=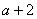 (
( 为常数);
为常数);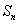 是
是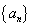 的前
的前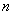 项和,且
项和,且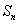 是
是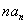 与
与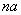 的等差中项。(1)求
的等差中项。(1)求 ;
;
(2)猜想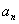 的表达式,并用数学归纳法加以证明;
的表达式,并用数学归纳法加以证明;
(3)求证以 为坐标的点
为坐标的点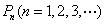 都落在同一直线上。
都落在同一直线上。
查看答案和解析>>
科目:高中数学 来源: 题型:
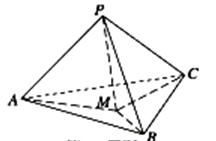
如图,在三棱锥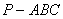 中,
中,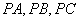 两两互相垂直,且
两两互相垂直,且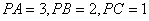 ,设
,设 是底面三角形
是底面三角形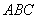 内一动点,定义:
内一动点,定义: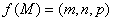 ,其中
,其中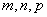 分别表示三棱锥
分别表示三棱锥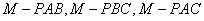 的体积,若
的体积,若 ,且
,且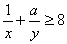 恒成立,则正实数
恒成立,则正实数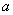 的最小值是( )
的最小值是( )
A . 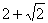 B .
B . 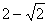 C.
C. 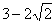 D.
D. 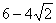
查看答案和解析>>
科目:高中数学 来源: 题型:
在某次数学复习检测中,老师从做过的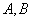 两套试卷中共挑选出6道试题,若这6道试题被随机地平均分给甲、乙、丙三位同学练习,且甲同学至少有一道试题来自
两套试卷中共挑选出6道试题,若这6道试题被随机地平均分给甲、乙、丙三位同学练习,且甲同学至少有一道试题来自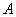 试卷的概率是
试卷的概率是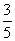 。
。
(1)求这6道试题来自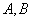 试卷各有几道试题;
试卷各有几道试题;
(2)若随机变量X表示甲同学的试题中来自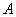 的试题数,求X分布列和数学期望。
的试题数,求X分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合A={x∈R|ax2-3x+2=0,a∈R}.
(1)若A是空集,求a的取值范围;
(2)若A中只有一个元素,求a的值,并把这个元素写出来;
(3)若A中至多有一个元素,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
“t≥0”是“函数f(x)=x2+tx-t在(-∞,+∞)内存在零点”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com