
在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则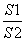 =
=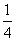 ,推广到空间可以得到类似结论;已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则
,推广到空间可以得到类似结论;已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则 =( )
=( )
A.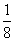 B.
B.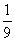 C.
C. D.
D.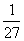
科目:高中数学 来源: 题型:
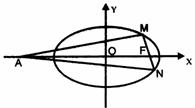
已知椭圆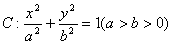 的离心率为
的离心率为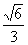 ,
,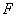 为椭圆在
为椭圆在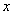 轴正半轴上的焦点,
轴正半轴上的焦点,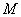 、
、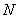 两点在椭圆
两点在椭圆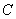 上,且
上,且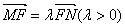 ,定点
,定点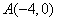 .
.
(I)求证:当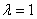 时
时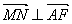 ;
;
(II)若当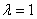 时有
时有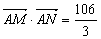 ,求椭圆
,求椭圆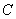 的方程;
的方程;
 (III)在(II)的椭圆中,当
(III)在(II)的椭圆中,当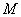 、
、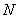 两点在椭圆
两点在椭圆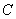 上运动时,试判断
上运动时,试判断 是否有最大值,若存在,求出最大值,并求出这时
是否有最大值,若存在,求出最大值,并求出这时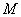 、
、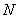 两点所在直线方程,若不存在,给出理由.
两点所在直线方程,若不存在,给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)—f(x)≤0,对任意正数a,b,若a<b,则必有( )
A.af(b)≤bf(a) B.bf(a)≤af(b) C.af(a)≤f(b) D.bf(b)≤f(a)
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{an}的前n项和为Sn,且方程x2-anx-an=0有一根为Sn-1,n=1,2,3…….
(1)求a1,a2;
(2)猜想数列{Sn}的通项公式,并给出严格的证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面几何里,有勾股定理:“设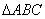 的两边AB、AC互相垂直,则
的两边AB、AC互相垂直,则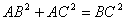 。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合A={x∈R|ax2-3x+2=0,a∈R}.
(1)若A是空集,求a的取值范围;
(2)若A中只有一个元素,求a的值,并把这个元素写出来;
(3)若A中至多有一个元素,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com