
分析 方法一:分离出m,构造关于m的函数,f(m)=x2+2(m-1)x+2m+6=2m(x+1)+x2-2x+6,分类讨论即可实数x的取值范围.
方法二,分离出m,构造关于m的函数,得到$\left\{\begin{array}{l}{f(0)>0}\\{f(2)>0}\end{array}\right.$,解得即可.
解答 解:方法一∵x2+2(m-1)x+2m+6>0在m∈[0,2]上总成立,
设f(m)=x2+2(m-1)x+2m+6=2m(x+1)+x2-2x+6,
当x+1>0时,f(m)为增函数,
∴x2-2x+6>0,
△=4-4×6<0,
∴x>-1,
当x+1=0时,即x2-2x+6=1+2+6=9>0,
当x+1<0时,f(m)为减函数,
∴4(x+1)+x2-2x+6>0,
即x2+2x+10>0,
△=4-4×10<0,
∴x<-1,
综上所述x的范围为R.
方法二:x2+2(m-1)x+2m+6>0在m∈[0,2]上总成立,
设f(m)=x2+2(m-1)x+2m+6=2m(x+1)+x2-2x+6,
则$\left\{\begin{array}{l}{f(0)>0}\\{f(2)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{{x}^{2}-2x+6>0}\\{{x}^{2}+2x+10>0}\end{array}\right.$,解得x∈R,
点评 本题考查函数的恒成立问题的应用,二次函数的单调性,基本不等式的应用,考查计算能力以及转化思想.


科目:高中数学 来源: 题型:解答题
| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 温差x (度) | 10 | 11 | 13 | 12 | 9 |
| 发芽数y(颗) | 15 | 16 | 17 | 14 | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1-\sqrt{5}}{2}$)∪(0,$\frac{\sqrt{5}-1}{2}$) | B. | ($\frac{1-\sqrt{5}}{2}$,0)∪($\frac{\sqrt{5}-1}{2}$,+∞) | C. | (-∞,$\frac{1-\sqrt{5}}{2}$)∪(0,$\frac{1+\sqrt{5}}{2}$) | D. | ($\frac{1-\sqrt{5}}{2}$,0)∪($\frac{1+\sqrt{5}}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{4}$,π)∪(-$\frac{π}{2}$,-$\frac{π}{4}$) | B. | ($\frac{π}{4}$,π) | C. | ($\frac{π}{4}$,π)∪(-π,-$\frac{3π}{4}$) | D. | (-$\frac{3π}{4}$,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
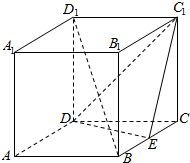 如图,在正方体ABCD-A1B1C1D1中,E是棱BC的中点.
如图,在正方体ABCD-A1B1C1D1中,E是棱BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com