练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知ab≠0，求证：a＋b＝1的充要条件是a3＋b3＋ab－a2－b2＝0.


    证明　充分性：∵a3＋b3＋ab－a2－b2

    ＝(a＋b)(a2－ab＋b2)－(a2－ab＋b2)

    ＝(a＋b－1)(a2－ab＋b2)

    ∴(a＋b－1)(a2－ab＋b2)＝0.

    又ab≠0，即a≠0且b≠0，

    ∴a2－ab－b2＝＋b2>0.

    ∴a＋b－1＝0，∴a＋b＝1.

    必要性：∵a＋b＝1，即a＋b－1＝0，

    ∴a3＋b3＋ab－a2－b2

    ＝(a＋b－1)(a2－ab＋b2)＝0.

    综上可知，当ab≠0时，

    a＋b＝1的充要条件是a3＋b3＋ab－a2－b2＝0.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    由“(a2＋a＋1)x>3，得x>”的推理过程中，其大前提是______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    命题“若x2＜1，则－1＜x＜1”的逆否命题是______．(填序号)

    ①若x2≥1，则x≥1或x≤－1；

    ②若－1＜x＜1，则x2＜1；

    ③若x＞1或x＜－1，则x2＞1；

    ④若x≥1或x≤－1，则x2≥1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b是实数，则“a>0且b>0”是“a＋b>0且ab>0”的________条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    命题“ax2－2ax＋3>0恒成立”是假命题，则实数a的取值范围是______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    判断下列命题的真假．

    (1)若x∈A∪B，则x∈B的逆命题与逆否命题；

    (2)若0<x<5，则|x－2|<3的否命题与逆否命题；

    (3)设a、b为非零向量，如果a⊥b，则a·b＝0的逆命题和否命题．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆的离心率为，焦点是(－3,0)，(3,0)，则椭圆方程为______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点P(3,4)是椭圆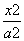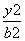＋＝1 (a>b>0)上的一点，F1、F2为椭圆的两焦点，若PF1⊥PF2，试求：

    (1)椭圆的方程；

    (2)△PF1F2的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     ________.

    查看答案和解析>>

    同步练习册答案