
| A. | $\frac{{{n^2}+n+1}}{2}$ | B. | $\frac{{{n^2}+n+2}}{2}$ | C. | $\frac{{{n^2}+n+3}}{2}$ | D. | $\frac{{{n^2}+n+4}}{2}$ |
分析 当n≥2时,利用an-a1=(an-an-1)+(an-1-an-2)+…+(a2-a1)计算可知an=$\frac{{n}^{2}+n+4}{2}$(n≥2),进而验证当n=1时是否成立即可.
解答 解:∵a1=3,an+1=an+n+1,
∴an+1-an=n+1,
∴当n≥2时,an-a1=(an-an-1)+(an-1-an-2)+…+(a2-a1)
=n+(n-1)+…+2
=$\frac{(n-1)(n+2)}{2}$,
∴an=$\frac{{n}^{2}+n-2}{2}$+3=$\frac{{n}^{2}+n+4}{2}$(n≥2),
又∵a1=3满足上式,
∴an=$\frac{{n}^{2}+n+4}{2}$,
故选:D.
点评 本题考查数列的通项,考查并项相加法,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
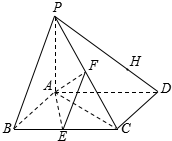 四棱锥P-ABCD底面是菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
四棱锥P-ABCD底面是菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2046 | B. | 2047 | C. | 2048 | D. | 2049 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 24 | C. | 16 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com