
分析 化简f(2)=a2,f(-2)=$\frac{1}{{a}^{2}}$+1,从而可得a2+$\frac{1}{{a}^{2}}$=$\frac{17}{4}$,从而求得.
解答 解:f(2)=a2,f(-2)=$\frac{1}{{a}^{2}}$+1,
故f(2)+f(-2)=a2+$\frac{1}{{a}^{2}}$+1=$\frac{21}{4}$,
则a2+$\frac{1}{{a}^{2}}$=$\frac{17}{4}$,
故a2=4或a2=$\frac{1}{4}$,
故a=2或a=$\frac{1}{2}$,
故答案为:2或$\frac{1}{2}$.
点评 本题考查了分段函数的应用及分类讨论的思想应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 集合M中共有2个元素 | B. | 集合M中共有2个相同元素 | ||
| C. | 集合M中共有1个元素 | D. | 集合M为空集 |
查看答案和解析>>
科目:高中数学 来源:2017届江苏南京市高三上学期学情调研数学试卷(解析版) 题型:填空题
已知圆柱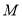 的底面半径为2,高为6,圆锥
的底面半径为2,高为6,圆锥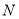 的底面直径和母线长相等,若圆柱
的底面直径和母线长相等,若圆柱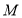 和圆锥
和圆锥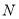 的体积相同,则圆锥
的体积相同,则圆锥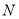 的高为 .
的高为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com