
分析 画出图形,确定三棱锥外接球的半径,然后求解外接球的表面积即可.
解答 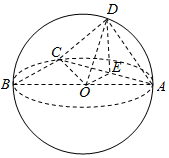 解:如图:AB=2,AD=1,CD=1,
解:如图:AB=2,AD=1,CD=1,
∴AC=$\sqrt{2}$,BC=$\sqrt{2}$,
取AC的中点E,AB的中点O,连结DE,OE,
∵平面DCA⊥平面ACB,DE⊥AC
∴DE⊥平面ACB,
∵DE=$\frac{\sqrt{2}}{2}$,OE=$\frac{\sqrt{2}}{2}$,
∴OD=1,
∴OB=OA=OC=OD,
∴OB=1,就是外接球的半径为1,
此时三棱锥外接球的表面积为4π•12=4π.
故答案为:4π.
点评 本题考查折叠问题,三棱锥的外接球的表面积的求法,考查空间想象能力以及计算能力.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:选择题
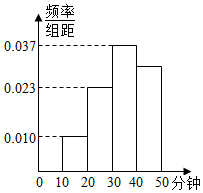 学校为了解学生每月购买学习用品方面的支出情况,抽取了n名学生进行调查,结果显示这些学生的支出(单位:元)都在[10,50]内,其频率分布直方图如图所示,其中支出在[10,30)内的学生有66人,则支出在[40,50]内的学生人数是( )
学校为了解学生每月购买学习用品方面的支出情况,抽取了n名学生进行调查,结果显示这些学生的支出(单位:元)都在[10,50]内,其频率分布直方图如图所示,其中支出在[10,30)内的学生有66人,则支出在[40,50]内的学生人数是( )| A. | 30 | B. | 40 | C. | 60 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在实施棚户区改造工程中,某居委会决定对AF地段上的危旧房进行推平改建,拟在EF地段上新建一幢居民安置楼,在EF安置楼正南面的AB地段上建一个活动中心,活动中心的侧面图由两部分构成,下部分ABCD是矩形,上部分是以CD为直径的半圆O,活动中心的规划设计需满足以下要求:①AE=30米;②AB≥AD;③当地“最斜光线”与水平线的夹角α满足tanα=$\frac{3}{4}$,活动中心在当地“最斜光线”照射下落在EF安置楼上的影长GE不超过$\frac{5}{2}$米.
如图,在实施棚户区改造工程中,某居委会决定对AF地段上的危旧房进行推平改建,拟在EF地段上新建一幢居民安置楼,在EF安置楼正南面的AB地段上建一个活动中心,活动中心的侧面图由两部分构成,下部分ABCD是矩形,上部分是以CD为直径的半圆O,活动中心的规划设计需满足以下要求:①AE=30米;②AB≥AD;③当地“最斜光线”与水平线的夹角α满足tanα=$\frac{3}{4}$,活动中心在当地“最斜光线”照射下落在EF安置楼上的影长GE不超过$\frac{5}{2}$米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-1,1) | C. | (-1,+∞) | D. | [-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com