
分析 椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)焦点在x轴上,四边形AFF1B为长方形.根据椭圆的定义:|AF|+|AF1|=2a,∠ABF=α,则∠AF1F=α.椭圆的离心率e=$\frac{2c}{2a}$=$\frac{1}{sinα+cosα}$=$\frac{1}{\sqrt{2}sin(α+\frac{π}{4})}$,α∈[$\frac{π}{6}$,$\frac{π}{4}$],$\frac{\sqrt{2}(\sqrt{3}+1)}{4}$≤sin(α+$\frac{π}{4}$)≤1,$\frac{\sqrt{2}}{2}$≤$\frac{1}{\sqrt{2}sin(α+\frac{π}{4})}$≤$\sqrt{3}$-1,即可求得椭圆离心率e的取值范围.
解答 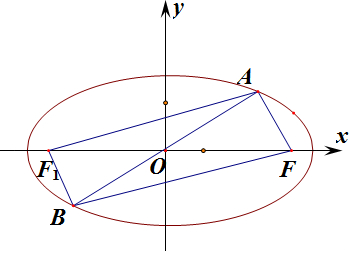 解:椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)焦点在x轴上,
解:椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)焦点在x轴上,
椭圆上点A关于原点的对称点为点B,F为其右焦点,设左焦点为F1,连接AF,AF1,BF,BF1,
∴四边形AFF1B为长方形.
根据椭圆的定义:|AF|+|AF1|=2a,
∠ABF=α,则:∠AF1F=α.
∴2a=2ccosα+2csinα
椭圆的离心率e=$\frac{2c}{2a}$=$\frac{1}{sinα+cosα}$=$\frac{1}{\sqrt{2}sin(α+\frac{π}{4})}$,α∈[$\frac{π}{6}$,$\frac{π}{4}$],
∴$\frac{5π}{12}$≤α+$\frac{π}{4}$≤$\frac{π}{2}$,
则:$\frac{\sqrt{2}(\sqrt{3}+1)}{4}$≤sin(α+$\frac{π}{4}$)≤1,
∴$\frac{\sqrt{2}}{2}$≤$\frac{1}{\sqrt{2}sin(α+\frac{π}{4})}$≤$\sqrt{3}$-1,
∴椭圆离心率e的取值范围:$[\frac{{\sqrt{2}}}{2},\sqrt{3}-1]$,
故答案为:$[\frac{{\sqrt{2}}}{2},\sqrt{3}-1]$.
点评 本题考查椭圆的定义,三角函数关系式的恒等变换,利用定义域求三角函数的值域,离心率公式的应用,属于中档题型.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
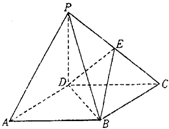 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.则二面角B-DE-C的平面角的余弦值是$\frac{\sqrt{3}}{3}$.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.则二面角B-DE-C的平面角的余弦值是$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com