
如图,在四棱锥V-ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,VA=1,E、F、G分别为VA、VB、BC的中点.
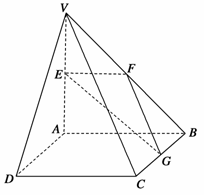
(1)求证:平面EFG∥平面VCD;
(2)当二面角V-BC-A、V-DC-A依次为45°、30°时,求直线VC与平面ABCD所成的角正弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知两个不同的平面α,β和两条不重合的直线m,n,则下列命题正确的是 ( )
A.若m∥n,n⊂α,则m∥α B.若a⊥β,α∩β=n,m⊥n,则m⊥β
C.若m⊂α,n⊂α,m∥β,n∥β,则α∥β D.若m⊥β,m⊂a则a⊥β
查看答案和解析>>
科目:高中数学 来源: 题型:
若函数f(x)=xcos x在(0,+∞)内的全部极值点按从小到大的顺序排列为a1,a2,…,an,…,则对任意正整数n必有( )
A.π<an+1-an<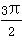 B.
B.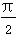 <an+1-an<π
<an+1-an<π
C.0<an+1-an<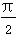 D.-
D.-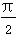 <an+1-an<0
<an+1-an<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com