
(本小题满分14分)已知函数 ,
, ,其中
,其中 且
且 .
.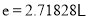 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当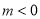 时,求函数
时,求函数 的单调区间和极小值;
的单调区间和极小值;
(Ⅱ)当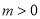 时,若函数
时,若函数 存在
存在 三个零点,且
三个零点,且 ,试证明:
,试证明:
 ;
;
(Ⅲ)是否存在负数 ,对
,对 ,
, ,都有
,都有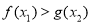 成立?若存在,求出
成立?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(Ⅰ) 的单调递减区间是
的单调递减区间是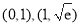 ,单调递增区间是
,单调递增区间是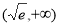 ;
; ;(Ⅱ)见解析;(Ⅲ)存在
;(Ⅱ)见解析;(Ⅲ)存在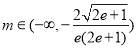
【解析】
试题分析:(Ⅰ)直接利用导数可得单调区间和极小值;(Ⅱ)函数存在三个零点,表示极大值g(0)大于零而极小值g(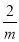 )小于零,得到m的范围,进而得到g(-1)和g(e)的范围,由此得出a,b,c满足的不等关系;(Ⅲ)由题意,
)小于零,得到m的范围,进而得到g(-1)和g(e)的范围,由此得出a,b,c满足的不等关系;(Ⅲ)由题意,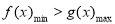 ,而
,而 ,
, ,∴
,∴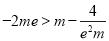 ,解出m的范围即可.
,解出m的范围即可.
试题解析:(Ⅰ) (
(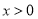 且
且 ).
).
∴由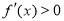 ,得
,得 ;由
;由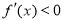 ,得
,得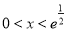 ,且
,且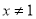 . 1分
. 1分
∴函数 的单调递减区间是
的单调递减区间是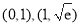 ,单调递增区间是
,单调递增区间是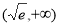 . 2分
. 2分
∴ . 1分
. 1分
(Ⅱ) .
.
∴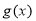 在
在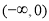 上单调递增,
上单调递增, 上单调递减,
上单调递减, 上单调递增.
上单调递增.
∵函数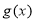 存在三个零点.
存在三个零点.
∴ .
.
∴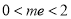 3分
3分
由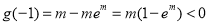 .
.
∴ . 1分
. 1分
综上可知,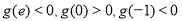 ,
,
结合函数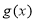 单调性及
单调性及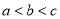 可得:
可得: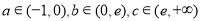 .
.
即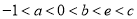 ,得证. 1分
,得证. 1分
(Ⅲ)由题意,只需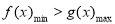
∵
由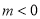 ,∴函数
,∴函数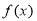 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
∴ . 2分
. 2分
∵
由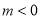 ,∴函数
,∴函数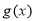 在
在 上单调递增,
上单调递增, 上单调递减.
上单调递减.
∴ . 2分
. 2分
∴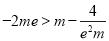 ,不等式两边同乘以负数
,不等式两边同乘以负数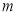 ,得
,得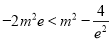 .
.
∴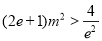 ,即
,即 .
.
由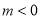 ,解得
,解得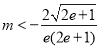 .
.
综上所述,存在这样的负数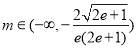 满足题意. 1分
满足题意. 1分
考点:利用导数研究函数性质,函数的单调性,极值,范围问题,恒成立问题


科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
函数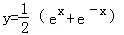 的导数是( )
的导数是( )
A.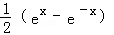 B.
B.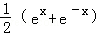 C.ex﹣e﹣x D.ex+e﹣x
C.ex﹣e﹣x D.ex+e﹣x
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:解答题
(本小题满分12分)口袋中装有除颜色,编号不同外,其余完全相同的2个红球,4个黑球.现从中同时取出3个球.
(Ⅰ)求恰有一个黑球的概率;
(Ⅱ)记取出红球的个数为随机变量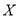 ,求
,求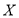 的分布列和数学期望
的分布列和数学期望 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市黄浦区高三上学期期终调研测试文科数学试卷(解析版) 题型:选择题
给定空间中的直线l及平面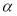 ,条件“直线l与平面α内的无数条直线都垂直”是“直线l与平面α垂直的( ).
,条件“直线l与平面α内的无数条直线都垂直”是“直线l与平面α垂直的( ).
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.非充分非必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com