
分析 (1)根据导数的几何意义,即可求出;
(2)先求导,再分类讨论,根据导数和函数的极值的关系即可求出.
解答 解:(1)∵f(x)=$\frac{1}{2}$x2-(a+1)x+a(1+lnx),
∴f′(x)=x-(a+1)+$\frac{a}{x}$,
∵曲线y=f(x)在(2,f(2))处与直线y=-x+1垂直,
∴f′(2)=2-(a+1)+$\frac{a}{2}$=1,
∴a=0,
∴f(2)=2-2=0,
∴切线方程为y=x-2,即x-y-2=0
(2)∵$f'(x)=x-a-1+\frac{a}{x}=\frac{(x-1)(x-a)}{x}(x>0)$,
当0<a<1时,函数在(a,1)上单调递减,在(0,a),(1,+∞)上单调递增,
故f(x)在x=1处取得极小值$-\frac{1}{2}$,在x=a处取得极大值$-\frac{1}{2}{a^2}+alna$,
当a=1时,f'(x)≥0,函数f(x)在(0,+∞)上单调递增,此时函数无极值,
当a>1时,函数在(1,a)上单调递减,在(0,1),(a,+∞)上单调递增,
故f(x)在x=1处取得极大值$-\frac{1}{2}$,在x=a处取得极小值$-\frac{1}{2}{a^2}+alna$
点评 本题考查了导数的几何意义和导数和最值的关系,以及分类讨论讨论的关系,属于中档题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学科 学生 | A | B | C | D | E |
| 数学成绩x | 88 | 76 | 73 | 66 | 63 |
| 物理成绩Y | 78 | 68 | 70 | 64 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
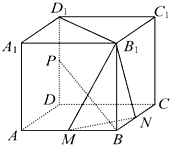 如图,正方体ABCD-A1B1C1D1中,P,M,N分别为棱DD1,AB,BC的中点.
如图,正方体ABCD-A1B1C1D1中,P,M,N分别为棱DD1,AB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com