练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．“a＞0”是“$a+\frac{2}{a}≥2\sqrt{2}$”的（　　）
    A．充分而不必要条件B．必要而不充分条件
    C．充要条件D．既不充分也不必要条件

    分析 根据充分必要条件的定义结合不等式的性质判断即可．

    解答 解：由a＞0，得a+$\frac{2}{a}$≥2$\sqrt{a•\frac{2}{a}}$=2$\sqrt{2}$，是充分条件，
    由a+$\frac{2}{a}$≥2$\sqrt{2}$，得：a＞0，
    故a＞0”是“$a+\frac{2}{a}≥2\sqrt{2}$”的充要条件，
    故选：C．

    点评 本题考查了充分必要条件，考查不等式的性质，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．实数x，y，a，b满足xy=2，a+2b=0，则（x-a）2+（y-b）2的最小值为$\frac{16}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．18、甲、乙两位同学参加数学文化知识竞赛培训，现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次，记录如下：
    甲：82 81 79 78 95 88 93 84
    乙：92 95 80 75 83 80 90 85
    （Ⅰ）用茎叶图表示这两组数据；
    （Ⅱ）现要从中选派一人参加正式比赛，从所抽取的两组数据求出甲、乙两位同学的平均值和方差，据此你认为选派哪位同学参加比赛较为合适？
    （Ⅲ）若对加同学的正式比赛成绩进行预测，求比赛成绩高于80分的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知集合A={0，2，4}，B={x|3x-x2≥0}，则集合A∩B的子集个数为（　　）
    A．2B．3C．4D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知△ABC的三个内角A，B，C所对的边分别为a，b，c，且满足$\sqrt{3}ccos（2016π-B）-sin（2017π+C）=0$．
    （1）求角B的大小；
    （2）若动点D在△ABC的外接圆上，且点D，B不在AC的同一侧，AC=7，试求△ACD面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．如图1，在直角梯形ABCD中，AB∥DC，∠BAD=90°，AB=AD=$\frac{1}{2}CD$=1，如图2，将△ABD沿BD折起来，使平面ABD⊥平面BCD，设E为AD的中点，F为AC上一点，O为BD的中点．
    （Ⅰ）求证：AO⊥平面BCD；
    （Ⅱ）若AF=2FC，求三棱锥A-BEF的体积．

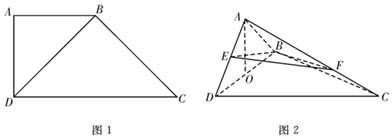
    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

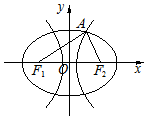    5．如图，椭圆与双曲线有公共焦点F1，F2，它们在第一象限的交点为A，且AF1⊥AF2
    ∠AF1F2=30°，则椭圆与双曲线的离心率的之积为（　　）
    A．2B．$\sqrt{3}$C．$\frac{1}{2}$D．$\frac{\sqrt{3}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．为选拔选手参加“中国谜语大会”，某中学举行了一次“谜语大赛”活动．为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数作为样本（样本容量为n）进行统计．按照[50，60），[60，70），[70，80）[80，90），[90，100]的分组作出频率分布直方图如同1，并作出样本分数的茎叶图如图2（图中仅列出了得分在[50，60），[90，100]的数据）．

    （Ⅰ）求样本容量n和频率分布直方图中的x，y的值；
    （Ⅱ）分数在[90，100]的学生设为一等奖，获奖学金500元；分数在[80，90）的学生设为二等奖，获奖学金200元．已知在样本中，获一、二等奖的学生中各有一名男生，则从剩下的女生中任取三人，求奖学金之和大于600的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．某校对学生的思想品德、学业成绩、社会实践能力进行综合评价，思想品德、学业成绩、社会实践能力评价指数分别记为x，y，z，每项评价指数都为1分、2分、3分、4分、5分五等，综合评价指标S=x+y+z，若S≥13，则该学生为优秀学生．现从该校学生中，随机抽取10名学生作为样本，分为A，B两组，其评价指数列表如下：
                                                                    A组
    学生编号A1A2A3A4A5
    评价指数（x，y，z）（3，4，3）（4，3，4）（4，4，2）（4，3，5）（4，5，4）
    B组
    学生编号 B1B2B3B4B5
    评价指数（x，y，z）（3，5，3）（4，3，2）（5，4，4）（5，4，5）（4，5，3）
    （1）从A，B两组中各选一名学生，依次记为甲、乙，求乙的综合评价指标大于甲的综合评价指标的概率；
    （2）若该校共有1500名学生，估计该校有多少名优秀学生．

    查看答案和解析>>

    同步练习册答案