Question

2．已知直线l与椭圆C：$\frac{x^2}{4}+{y^2}=1$交于A，B两点，且|AB|=2，则直线l与圆x²+y²=1的位置关系为（　　）

• A． 相离
• B． 相交
• C． 相切
• D． 相交或相切

Answer 1

分析 画出椭圆与圆的图形，通过线段AB的距离，判断位置关系即可．

解答 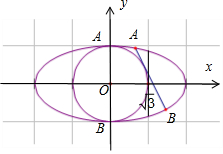解：椭圆C：$\frac{x^2}{4}+{y^2}=1$与圆x²+y²=1的图形如图，AB的距离为2，显然AB是椭圆的短轴长时，直线l与椭圆相交，椭圆的通经长为：$\sqrt{3}$，
在图形中存在|AB|=2，直线l与圆相切，设直线l：y=kx+m，由题意可得：$\frac{|m|}{\sqrt{1+{k}^{2}}}=1$…①，$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$，消去y整理可得（1+4k²）x²+8kmx+4m²-4=0，可得x₁+x₂=$\frac{-8mk}{1+4{k}^{2}}$，x₁x₂=$\frac{4{m}^{2}-4}{1+4{k}^{2}}$，
|AB|=$\sqrt{1+{k}^{2}}|{x}_{2}-{x}_{1}|$=2，代入x₁+x₂，x₁x₂，化简整理可得：$\frac{2\sqrt{1+{k}^{2}}}{1+4{k}^{2}}\sqrt{4{k}^{2}-{m}^{2}+1}=1$…②
联立①②消去m可得：$\frac{2\sqrt{1+{k}^{2}}}{1+4{k}^{2}}\sqrt{3{k}^{2}}=1$，化简可得：4k⁴-4k²+1=0，解得k=$±\frac{\sqrt{2}}{2}$，
所以转化的直线l存在，由4条．
所以直线与圆的位置关系是相交或相切．
故选：D．

点评 本题考查椭圆的简单性质以及圆的图形的应用，考查数形结合分析问题解决问题的能力．