Question

17．已知f（x）是定义在R上的奇函数，当x＞0时，f（x）=$\frac{1}{3}$x³+ax（a∈R），且曲线f（x）在x=$\frac{1}{2}$处的切线与直线y=-$\frac{3}{4}$x-1平行．
（Ⅰ）求a的值及函数f（x）的解析式；
（Ⅱ）若函数y=f（x）-m在区间[-3，$\sqrt{3}$]上有三个零点，求实数m的取值范围．

Answer 1

分析 （Ⅰ）首先求得导函数，然后利用导数的几何意义结合两直线平行的关系求得a的值，由此求得函数f（x）的解析式；
（Ⅱ）将问题转化为函数f（x）的图象与y=m有三个公共点，由此结合图象求得m的取值范围．

解答 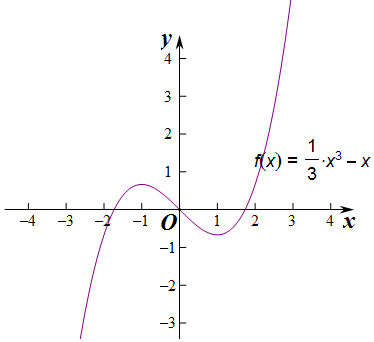解：（Ⅰ）当x＞0时，f′（x）=x²+a，
因为曲线f（x）在x=$\frac{1}{2}$处的切线与直线y=-$\frac{3}{4}$x-1平行，
所以f′（$\frac{1}{2}$）=$\frac{1}{4}$+a=-$\frac{3}{4}$，解得a=-1，
所以f（x）=$\frac{1}{3}$x³-x，
设x＜0则f（x）=-f（-x）=$\frac{1}{3}$x³-x，
又f（0）=0，所以f（x）=$\frac{1}{3}$x³-x．
（Ⅱ）由（Ⅰ）知f（-3）=-6，f（-1）=$\frac{2}{3}$，f（1）=-$\frac{2}{3}$，f（$\sqrt{3}$）=0，
所以函数y=f（x）-m在区间[-3，$\sqrt{3}$]上有三个零点，
等价于函数f（x）在[-3，$\sqrt{3}$]上的图象与y=m有三个公共点．
结合函数f（x）在区间[-3，$\sqrt{3}$]上大致图象可知，实数m的取值范围是（-$\frac{2}{3}$，0）．

点评 本题考查导数知识的综合运用，考查导数的几何意义，考查数形结合的数学思想，属于中档题．