
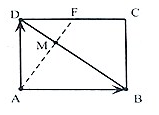
 ��ͼ���ھ���ABCD�У�F�DZ�CD���е㣬M��AF��BD���㣬��$\overrightarrow{AB}$=$\overrightarrow{a}$��$\overrightarrow{AD}$=$\overrightarrow{b}$
��ͼ���ھ���ABCD�У�F�DZ�CD���е㣬M��AF��BD���㣬��$\overrightarrow{AB}$=$\overrightarrow{a}$��$\overrightarrow{AD}$=$\overrightarrow{b}$���� ��1��$\overrightarrow{AF}=\overrightarrow{AD}+\overrightarrow{DF}$=$\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}=\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}$��
��2���ɡ�DMF�ס�BMA��
�ɵ�M�ǶԽ���BD�����ȷֵ㣮
���  �⣺��1��$\overrightarrow{AF}=\overrightarrow{AD}+\overrightarrow{DF}$=$\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}=\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}$��
�⣺��1��$\overrightarrow{AF}=\overrightarrow{AD}+\overrightarrow{DF}$=$\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}=\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}$��
֤������2����DF��AB�����DMF�ס�BMA��
��$\frac{DF}{AB}=\frac{DM}{MB}=\frac{1}{2}$��
��M�ǶԽ���BD�����ȷֵ㣮
���� ���⿼����ƽ���������������㡢���������ƣ������е��⣮


 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | 1 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | δ���� | �ܼ� | |
| û����ҩ | 20 | 30 | 50 |
| ����ҩ | x | y | 50 |
| �ܼ� | M | N | 100 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 54�� | B�� | 48�� | C�� | 42�� | D�� | 36�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com