
分析 ( I)求出:当a=-$\frac{1}{2}$时,函数的分段函数形式,求出函数的最小值,然后证明不等式lnf(x)>1成立;
(II)利用绝对值的几何意义求出函数的最小值,列出不等式求解即可.
解答 解:(I)证明:由$f(x)\;=|{x-\frac{5}{2}}|+|{x+\frac{1}{2}}|=\left\{\begin{array}{l}-2x+2x<-\frac{1}{2}\\ 3-\frac{1}{2}≤x≤\frac{5}{2}\\ 2x-2\;\;x>\frac{5}{2}\end{array}\right.$,
得函数f(x)的最小值为3,从而f(x)≥3>e,所以lnf(x)>1成立.
( II)由绝对值的性质得$f(x)=|{x-\frac{5}{2}}|+|{x-a}|≥|{(x-\frac{5}{2})-(x-a)}|=|{a-\frac{5}{2}}|$,
所以f(x)最小值为$|{\frac{5}{2}-a}|$,从而$|{\frac{5}{2}-a}|≤a$,
解得$a≥\frac{5}{4}$,
因此a的取值范围为$[\frac{5}{4},+∞)$.
点评 本题考查绝对值的几何意义,不等式的证明,函数的最值的应用,考查转化思想以及计算能力.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:解答题
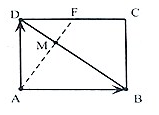 如图,在矩形ABCD中,F是边CD的中点,M是AF与BD交点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$
如图,在矩形ABCD中,F是边CD的中点,M是AF与BD交点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在边长为1的等边△ABC中,AA1=BB1=CC1=x(0<x<1),△A1B1C1的面积为y.
如图所示,在边长为1的等边△ABC中,AA1=BB1=CC1=x(0<x<1),△A1B1C1的面积为y.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2-$\frac{2\sqrt{3}}{3}$,2$+\frac{2\sqrt{3}}{3}$] | B. | [2-$\frac{2\sqrt{3}}{3}$,3] | C. | [1,2$+\frac{2\sqrt{3}}{3}$] | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,求此点取自黑色部分的概率.
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,求此点取自黑色部分的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com